Calendrier Mathématique Août 2020
Lundi 3 Août

L’angle de la hauteur issue de C et de (AB) est 90°.
Comme la somme des angles d’un triangle est 180°, ∠DAH = 180 - 97 - 90 = 20°
La bissectrice coupe un angle en deux, donc ∠BAC = 2 × 20 = 40°.
On en déduit l’angle ∠BCA = 180 - 60 - 40 = 80°.
réponse: 80°
Mardi 4 Août
En développant:
- ab + ac = 152
- bc + ba = 162
- ca + cb = 170
Notons x = ab, y = bc et z = ca. Les équations peuvent s’écrire:
- x + z = 152
- y + x = 162
- z + y = 170
Ce qui se résout en: x = 72, y = 90, z = 80
xyz = ab × bc × ca = (abc)² = 72 × 90 × 80 = 518400 = 720²
Nota: la solution positive au système initial est: a = 8, b = 9, c = 10
réponse: 720
Mercredi 5 Août
| mouvement | ① 2 l | ② 5/4 l | ③ 3/4 l |
|---|---|---|---|
| départ | 2,00 | 0,00 | 0,00 |
| ① dans ② | 0,75 | 1,25 | 0,00 |
| ② dans ③ | 0,75 | 0,50 | 0,75 |
| ③ dans ① | 1,50 | 0,50 | 0,00 |
| ② dans ③ | 1,50 | 0,00 | 0,50 |
| ① dans ② | 0,25 | 1,25 | 0,50 |
| ② dans ③ | 0,25 | 1,00 | 0,75 |
| ③ dans ① | 1,00 | 1,00 | 0,00 |
réponse: oui
Jeudi 6 Août
Soient r₁ et r₂ les rayons des deux cercles en centimètres.
A₁ - A₂ = π (r₁² - r₂²) = 72 π
r₁ + r₂ = 1800
(r₁ + r₂)(r₁ - r₂) = 72 ⇒ (r₁ - r₂) = 72 / 1800 = 1 / 25
2r₁ = 1800 + 1 / 25
On en déduit r₁ - 45001 / 50 et r₂ = 45001 / 50 = 1 / 25 = 44999 / 50
réponse: 44999 / 50 et 45001 / 50
Vendredi 7 Août
Comme 100 = 9 + 9 + 82, le plus petit nombre “centenaire” possible est 82. Il faut tester ensuite…
Le programme Python le fait pour nous.
#!/usr/bin/env python3
nb = 0
for a in range(80, 100):
for b in range(a, 100):
n1 = a + (b // 10) + (b % 10)
n2 = b + (a // 10) + (a % 10)
if n1 == n2 == 100:
print(a, b)
nb += 1
print("réponse:", nb)
Il y a donc cinq “paires centenaires”: (83, 89) (84, 88) (85, 87) (86, 86) (90, 91)
réponse: 5
Lundi 10 Août
Si Jean choisit le dé 4-0:
- 0 est toujours perdant (i.e. Léa gagne)
- 4 est perdant 5 fois sur 18 tirages possibles
- si Léa choisit le dé 1-5 elle a 2/3 de chance de gagner
2/6 + 4/6 × 5/18 = 14/27
Si Jean choisit le dé 3:
- 3 est perdant 4+2+3 = 9/18 = 1/2
- si Léa choisit le dé 0-4 elle a 2/3 de chance de gagner
Si Jean choisit le dé 6-2:
- 2 est perdant 4+6+3: 4/6 × 13/18 = 13/27
- 6 est toujours gagnant
- si Léa choisit le dé 3 elle a 2/3 de chance de gagner
Si Jean choisit le dé 5-1:
- 1 est perdant 4+6+6 fois: 3/6 × 16/18
- 5 est perdant 2 fois: 3/6 × 2/18
- si Léa choisit le dé 2-6 elle a 2/3 de chance de gagner
3/6 × 2/18 + 3/6 × 16/18 = 1/2
Soit au total:
1/4 × (14/27 + 1/2 + 13/27 + 1/2) = 1/4 × 2 = 1/2
Calcul de tous les tirages possibles par programme.
#!/usr/bin/env python3
from fractions import Fraction
des = [
[0, 0, 4, 4, 4, 4],
[3, 3, 3, 3, 3, 3],
[2, 2, 2, 2, 6, 6],
[1, 1, 1, 5, 5, 5],
]
total_nb = 0
total_lea_gagne = 0
max_lea_f = 0
# Jean choisit un dé
for de_jean in range(4):
des_lea = set(range(4))
des_lea.remove(de_jean)
# Léa choisit un dé parmi les trois restants
for de_lea in des_lea:
nb = 0
lea_gagne = 0
# Jean tire son dé
for tirage_jean in des[de_jean]:
# Léa tire son dé
for tirage_lea in des[de_lea]:
nb += 1
# Léa gagne si son tirage est supérieur à celui de Jean
if tirage_lea > tirage_jean:
lea_gagne += 1
f = Fraction(lea_gagne, nb)
# print(
# f"de_jean: {des[de_jean]} de_lea: {des[de_lea]} - "
# + f"lea_gagne: {lea_gagne}/{nb} = {f}"
# )
if f > max_lea_f:
max_lea_f = f
total_lea_gagne += lea_gagne
total_nb += nb
f = Fraction(total_lea_gagne, total_nb)
print(f"total_lea_gagne: {total_lea_gagne}/{total_nb} = {f}")
print(f"max_lea_f: {max_lea_f}")
réponse: Léa a p=1/2 chances de gagner. Si elle choisit bien son dé, elle a p=2/3 chances de gagner
Mardi 11 Août
Soit d le chiffre des dizaines de n et u celui des unités.
Ils sont solutions de l’équation:
d × u + d + u = 10 × d + u
d × u + d = 10 × d
u + 1 = 10 (car d ≠ 0)
Soit, u = 9 et d quelconque.
Autrement dit, tous les nombres qui se terminent par 9 entre 10 et 90.
réponse: 8
Mercredi 12 Août
₁ ₂ ₃ ₄ ₅ ₆
▲ ▲ ▲ ▲ ▲ ▲
▲ ▼ ▼ ▼ ▼ ▼ ①
▼ ▼ ▲ ▲ ▲ ▲ ②
▲ ▲ ▲ ▼ ▼ ▼ ③
▼ ▼ ▼ ▼ ▲ ▲ ④
▲ ▲ ▲ ▲ ▲ ▼ ⑤
▼ ▼ ▼ ▼ ▼ ▼ ⑥
Gagné
Programme du jeu écrit en Python.
#!/usr/bin/env python3
import sys
def read_single_keypress():
"""Waits for a single keypress on stdin.
This is a silly function to call if you need to do it a lot because it has
to store stdin's current setup, setup stdin for reading single keystrokes
then read the single keystroke then revert stdin back after reading the
keystroke.
Returns a tuple of characters of the key that was pressed - on Linux,
pressing keys like up arrow results in a sequence of characters. Returns
('\x03',) on KeyboardInterrupt which can happen when a signal gets
handled.
"""
import termios, fcntl, sys, os
fd = sys.stdin.fileno()
# save old state
flags_save = fcntl.fcntl(fd, fcntl.F_GETFL)
attrs_save = termios.tcgetattr(fd)
# make raw - the way to do this comes from the termios(3) man page.
attrs = list(attrs_save) # copy the stored version to update
# iflag
attrs[0] &= ~(
termios.IGNBRK
| termios.BRKINT
| termios.PARMRK
| termios.ISTRIP
| termios.INLCR
| termios.IGNCR
| termios.ICRNL
| termios.IXON
)
# oflag
attrs[1] &= ~termios.OPOST
# cflag
attrs[2] &= ~(termios.CSIZE | termios.PARENB)
attrs[2] |= termios.CS8
# lflag
attrs[3] &= ~(
termios.ECHONL | termios.ECHO | termios.ICANON | termios.ISIG | termios.IEXTEN
)
termios.tcsetattr(fd, termios.TCSANOW, attrs)
# turn off non-blocking
fcntl.fcntl(fd, fcntl.F_SETFL, flags_save & ~os.O_NONBLOCK)
# read a single keystroke
ret = []
try:
ret.append(sys.stdin.read(1)) # returns a single character
fcntl.fcntl(fd, fcntl.F_SETFL, flags_save | os.O_NONBLOCK)
c = sys.stdin.read(1) # returns a single character
while len(c) > 0:
ret.append(c)
c = sys.stdin.read(1)
except KeyboardInterrupt:
ret.append("\x03")
finally:
# restore old state
termios.tcsetattr(fd, termios.TCSAFLUSH, attrs_save)
fcntl.fcntl(fd, fcntl.F_SETFL, flags_save)
return tuple(ret)
def play(board, move):
if move >= 0 and move < len(board):
move = " " + "①②③④⑤⑥⑦⑧⑨⑩"[move]
else:
move = ""
line = " ".join("▲" if i > 0 else "▼" for i in board)
print(f"\033[32m{line}\033[0m{move}", end="\n")
if all(i == -1 for i in board):
return True
print("\033[2m" + " ".join("₁₂₃₄₅₆₇₈₉₀"[: len(board)]) + "\033[0m")
return False
print("\033[H\033[2J", end="") # clear
try:
size = int(sys.argv[1])
if size < 2 or size > 10:
raise ValueError
except (IndexError, ValueError):
size = 6
board = [1] * size
move = -1
while True:
if play(board, move):
print("Gagné")
break
key = "".join(read_single_keypress())
if len(key) != 1:
continue
if key in "xXqQ\03\033": # Echap, ^C, x, q pour quitter
break
if key == "R": # recommencer
board = [1] * len(board)
continue
move = "&é\"'(§è!çà".find(key)
if move == -1:
move = "1234567890".find(key)
if move == -1 or move >= len(board):
continue
board = [-v if i != move else v for i, v in enumerate(board)]
réponse: oui c’est possible
Jeudi 13 Août
$k=\frac{9n^2+31}{n^2+7}=\frac{9n^2+63-32}{n^2+7}=9-\frac{32}{n^2+7}$
Il faut donc que 𝑛²+7 divise 32.
- 𝑛=1: 𝑛²+7=8 ✅
- 𝑛=2: 𝑛²+7=11 et 11 ne divise pas 32 ❌
- 𝑛=3: 𝑛²+7=16 convient ✅
- 𝑛=4: 𝑛²+7=23 non ❌
- 𝑛=5: 𝑛²+7=32 ok ✅
réponse: 𝑛 = ±1 ±3 ±5
Vendredi 14 Août
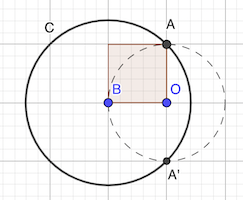
Le grand cercle de centre B a pour rayon BA avec AB diagonale du carré de côté r = OB = OA.
L’aire 𝒜 recherchée est l’aire du cercle de centre B de rayon r√2 diminuée de la moitié du cercle de centre O de rayon r et du segment AA’E du grand cercle.
Le segment AA’E a pour aire 𝒶 celle du secteur) ABA’ moins le triangle ABA’.
𝒶 = π (r√2)² / 4 - r × 2r / 2 = r² × (π / 2 - 1)
𝒜 = π (r√2)² - π (r²) / 2 - 𝒶 = r² × (2π - π / 2 - π / 2 + 1) = r² × (π + 1)
réponse: r² × (π + 1)
Lundi 17 Août
Les candidats de carré d’entiers sont 1, 4, 9 et 16. Soit:
- pour 1: 1-0 ⇒ 1 nombre (10)
- pour 4: 2-2 1-3 4-0 ⇒ 4 nombres (22 13 31 40)
- pour 9: 1-8 2-7 3-6 4-5 9-0 ⇒ 9 nombres (18 27 36 45 81 72 63 54 90)
- pour 16: 7-9 8-8 ⇒ 3 nombres (79 97 88)
Programme Python de vérification.
#!/usr/bin/env python3
carres = list(n * n for n in range(5))
nb = 0
for n in range(10, 100):
d, u = divmod(n, 10)
if d + u in carres:
print(n)
nb += 1
print("réponse:", nb)
réponse: 17
Mardi 18 Août
Soit respectivement p < m < g le poids des petits, moyens et grands poissons, et X le nombre de poissons de moyenne taille recherché.
3p + X × m + 3g = P
P - 3g = P - 0.35 × P = 0.65 P ⇒ 3g = 7 / 20 × P
0.65 × P - 3p = 0.65 × P - 5 / 13 × 0.65 P ⇒ 3p = 1 / 4 × P
D’où: 1 / 4 × P + X × m + 7 / 20 × P = P
X × m = P × (1 - 3 / 5) = 2 / 5 × P
On doit avoir X entier et 1 / 12 P < m < 7 / 60 P
En remplaçant m par 2 / 5 × P / X:
5 / 60 < 2 / (5 × X) < 7 / 60
12 > 5 / 2 X > 60 / 7
24 / 5 > X > 24 / 7
X = 4
réponse: 4
Mercredi 19 Août
Pour $n \leq 1$, $2^{2^n}+9$ vaut:
- $n = 0 : 2^{2^0} + 9 = 2^1 + 9 = 11$ ✅
- $n = 1 : 2^{2^1} + 9 = 2^2 + 9 = 13$ ✅
Pour $n \geq 2$: $2^{2^n} = 2^{4 \times 2^{n-2}} = 16^{n-2}$
Or, toutes les puissances de 16 se terminent par une puissance du chiffre de l’unité, à savoir 6:
$(10d+u)^n = 100 d^2 + 20d+ u^2 = 10 D+u^2$
Et plus généralement:
\[(10d+u)^n=\sum_{k=0}^n {n \choose k} (10d)^{k} u^{n-k}=\sum_{k=1}^n {n \choose k} (10d)^{k} u^{n-k}+u^n=10D+u^n\]Et comme $6\times6=36$ se termine aussi par 6, c’est invariablement 6 à la fin. Ajouté 9, le nombre se terminera toujours par 5, et est donc divisible par 5.
réponse: n = 0 ou n = 1
Jeudi 20 Août
365 mod 52 = 1 : on “avance” d’un jour de semaine par année non bissextile, et de deux sinon.
- 2021 n’est pas bissextile, vendredi 20 août 2021
- 2022 samedi 20 août 2022
- 2023 dimanche 20 août 2023
- 2024 est bissextile mardi 20 août 2024
- 2025 mercredi 20 août 2025
- 2026 jeudi 20 août 2026
Vérification avec programme en Python.
#!/usr/bin/env python3
from datetime import datetime
annee = 2020
ref = datetime(2020, 8, 20).weekday()
while True:
annee += 1
d = datetime(annee, 8, 20)
print(f"{d.year} : {d.strftime('%A')}")
if d.weekday() == ref:
break
réponse: 2026
Vendredi 21 Août
Le petit rectangle a un rapport largeur/hauteur égal à 2 puisqu’il “contient” deux cercles côte à côte. Calculons ses dimensions dont on déduira le diamètre des cercles (égal à la hauteur du petit rectangle) et ainsi le périmètre du grand rectangle.
2 (l + h) = 2 × (2h + h) = 6h = 60 cm
D’où h = 10 cm et 𝑃 = 2 × (3h + 2h) = 10h = 100 cm
réponse: 100 cm
Lundi 24 Août
Il faut que $0\leq 1 - x$ et $0\leq x$ pour que les racines carrées soient définies. Donc $0 \leq x \leq 1$.
On en déduit que: $0\leq\left(\sqrt{x}\right)^{2019} \leq 1$ et $0\leq\left(\sqrt{1-x}\right)^{2020} \leq 1 - x$
Soit: $0\leq\left(\sqrt{x}\right)^{2019} + \left(\sqrt{1-x}\right)^{2020} \leq 1$. Cependant 0 n’est pas possible car les deux racines ne peuvent être nulles en même temps. On a donc:
\[\left(\sqrt{x}\right)^{2019} + \left(\sqrt{1-x}\right)^{2020} =1\]Il y a deux solutions évidentes: $x = 0$ et $x = 1$.
La fonction est décroissante puis croissante sur l’intervalle [0; 1]. Les deux solutions sont donc les seules.
réponse: 0 et 1
Mardi 25 Août
C’est l’ensemble des nombres 1x0 ou x10 avec x ≠ 9 qui soient multiples de 30.
[100+i*10 for i in range(10) if (100+i*10)%30==0]
[10+i*100 for i in range(10) if (10+i*100)%30==0]
[i for i in range(100,1000) if i%30==0 and str(i).find('1')!=-1 and str(i).find('9')==-1]
réponse: 120, 150, 180, 210, 510, 810
Mercredi 26 Août
Soit x l’âge de Xavier.
(x - 55) × (x + 55) = x² - 55² = p³
Admettons qu’il a moins de 120 ans. Il faut donc trouver un cube de premier inférieur à 11375 < 23³ = 12167.
On va tester les premiers inférieurs à 23 un par un à l’aide d’un programme en Python.
#!/usr/bin/env python3
from sympy.ntheory import sieve
sieve.extend(23)
primes = sieve._list
cubes = [n ** 3 for n in sieve._list]
for n in range(55, 121):
if (n - 55) * (n + 55) in cubes:
print("réponse:", n)
break
réponse: 66 ans
Jeudi 27 Août
Code source du dessin réalisé avec TikZ en LaTeX .
réponse: cf. damier
Vendredi 28 Août
\[\begin{aligned} a_2&=1\times(a_0+a_1)=1\times(1+1)=2 \\ a_3&=2\times(a_1+a_2)=2\times(1+2)=6 \\ a_4&=3\times(a_2+a_3)=3\times(2+6)=24 \\ \end{aligned}\]$a_n$ semble être la fonction factorielle. Montrons que $a_n=n!$ par récurrence: c’est vrai pour $a_n, n\leq 4$, on suppose que c’est vrai pour $n$ et on vérifie pour $n+1$:
\[\begin{aligned} a_{n+1}&=n(a_{n-1}+a_n) \\ &=n \bigl((n-1)!+n! \big) \\ &=n!+n\times n! \\ &=n!\times(1+n) \\ &=(n+1)! \\ \end{aligned}\]Donc, à partir de 5!, le chiffre des unités est 0 car il y a 2×5=10 comme facteur.
On peut le vérifier à l’aide d’un programme en Python.
#!/usr/bin/env python3
from math import factorial
a0, a1 = 1, 1
for n in range(1, 2021):
a = n * (a0 + a1)
n += 1
a1, a0 = a, a1
if n <= 6 or n == 2020:
s = str(a)
if len(s) > 20:
s = "[...]" + s[-20:]
print(f"a({n}) = {s}", factorial(n) == a)
réponse: 0
Lundi 31 Août
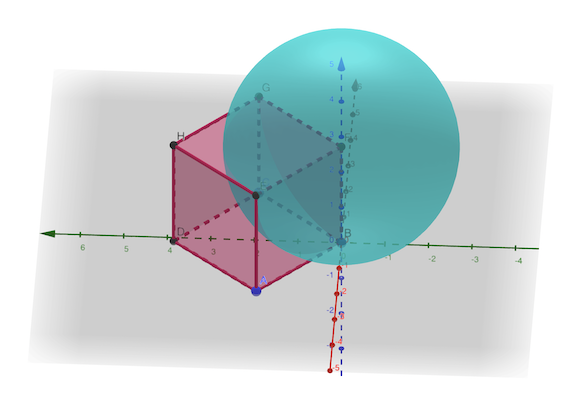
Il y a un quart de l’hémisphère sud qui intercepte le carré.
réponse: 1 / 8