Calendrier Mathématique Décembre 2020
Mardi 1 Décembre
Pour calculer l’aire de l’octogone, il faut déterminer la longueur des côtés des triangles isocèles rectangles.
Sachant que le carré central fait 4 cm², ses côtés font 2 cm. Les rectangles du bord ont pour dimension (2, a) et les triangles 2 cm en hypoténuse et a pour les deux autres côtés.
Pythagore: a² + a² = 2² ⇒ a = √2
L’aire de l’octogone est donc la somme de:
- 4 (carré central)
- 4 × √2 × 2 (rectangles périphériques)
- 4 × √2 × √2 / 2 (triangles isocèles rectangles)
A = 4 + 8 √2 + 4 = 8 + 8 √2
réponse: 8 + 8 √2 cm²
Mercredi 2 Décembre
Regroupons et calculons les facteurs deux par deux (pour n pair ≥ 2) :
\[\left(1+\frac{1}{n}\right)\times\left(1-\frac{1}{n+1}\right) = \left(\frac{n+1}{n}\right)\times\left(\frac{n+1-1}{n+1}\right)=\frac{(n+1)\times n}{n\times(n+1)}=1\]Il y a un nombre impair de facteurs, le dernier étant $1+\frac{1}{1000}=\frac{1001}{1000}$. Comme le produit des précédents vaut 1, le résultat est celui-ci.
réponse: 1001 / 1000
Jeudi 3 Décembre
En remplaçant:
\[ab+ac+bc = ab+ac+a^2-a+1 = a(a+b+c)-a+1=a-a+1=1\]réponse: 1
Vendredi 4 Décembre
Il y a 21 chances sur 25 de prendre une première calculette non défectueuse. Puis 20 chances sur 24 d’en prendre une deuxième. Etc.
\[\frac{21}{25}\times\frac{20}{24}\times\frac{19}{23}\times\frac{18}{22}=\frac{969}{2530}\]réponse: 969 / 2530
Lundi 7 Décembre
Ce sont certains nombres multiples de 3 × 5 × 7 = 105 (pas ceux de 2 à cause de des conditions de l’énoncé).
105 × 3, 5, 7, 9. A partir, de 11 c’est trop grand.
réponse: 105, 315, 525, 735, 945
Mardi 8 Décembre
Problème similaire au 13 novembre.
Il y a 3⁴ = 81 nombres.
27 × (3 + 5 + 7) × 1111 = 449955
réponse: 449955
Mercredi 9 Décembre
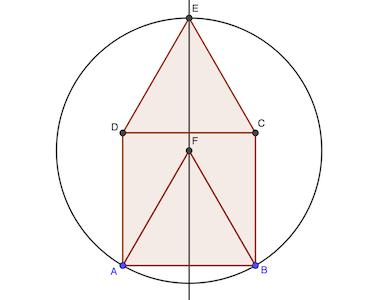
Le point F centre du cercle doit être tel que FA = FB = FE et F sur la médiatrice du segment CD.
En construisant le losange ADEF, on a bien FA = FE = DE = AD.
Le rayon du cercle est donc 1 cm.
réponse: 1 cm
Jeudi 10 Décembre
\[\begin{aligned} &2 clou + 5 vis + 8 cheville = 150 &(1)\\ &1 clou + 3 vis + 5 cheville = 80 &(2) \\ \\ &2\times(2)-(1) = vis+2cheville=10 \\ &\implies vis=10-2cheville&(3) \\ &\implies vis+2cheville=10&(4) \\ \end{aligned}\]En utilisant (2), (3) puis (4):
\[\begin{aligned} &clou+vis+cheville\\ &=(80-3vis-5cheville)+(10-2cheville)+cheville\\ &=90-3vis-6cheville\\ &=90-3(vis+2cheville)\\ &=90-3\times 10 = 60 \end{aligned}\]Une autre manière de faire (mais qui revient in fine au même) est de fixer arbitrairement une valeur d’une inconnue puisque le système de deux équations à trois inconnues admet une infinie de solutions.
Soit $cheville = 0$. On a alors:
\[\begin{aligned} &2 clou + 5 vis=150\\ &1 clou + 3 vis=80 \\ &\implies \begin{cases}vis=10 \\ clou=50 \end{cases} \end{aligned}\]Et donc:
\[clou+vis+cheville=50+10+9=60\]réponse: clou + vis + cheville = 60 g
Vendredi 11 Décembre
\[\frac{a^2+b^2+1}{ab+a+b}=-2 \iff a^2+b^2+1+2ab+2a+2b=(a+b)^2+1+2(a+b)=0\]Soit $x=a+b$. L’équation devient: $x^2+2x+1=0$.
La racine double du polynome du deuxième degré est $x=-1$.
réponse: a + b = -1
Lundi 14 Décembre
97 + y² = x²
x² - y² = (x + y)(x - y) = 97 × 1
97 est premier. Donc la seule possibilité est x + y = 97 et x - y = 1. Soit x = 49 et y = 48.
D’où x² + y² = 4705
réponse: 4705
Mardi 15 Décembre
On a:
(100 + x - y) + (50 + x +z) + (120 -x) + (100 + x + y) + (80 + x - z) = 3x + 450 = 180 (5 - 2) / 5 = 540° (modulo 360)
Car la somme des angles internes d’un polygone est π (n-2).
Donc x = (540 - 450) / 3 = 39°
réponse: x = 30°
Mercredi 16 Décembre
Eve enlève toute une pile puis enlève le même nombre de jetons que Bob dans l’autre pile. Bob perdra.
réponse: Eve
Jeudi 17 Décembre
Comme 175 = 5 × 5 × 7, les seuls nombres à trois chiffres non nuls donc le produit est multiple de 175 sont ceux avec 557.
Il y a 9 nombres avec deux 0 (100, 200, etc.)
Il y a 9 × 9 nombres avec un 0 chiffre des dizaines, et autant avec un 0 en unité.
Soit 3 + 9 + 81 × 2 = 174
réponse: 557 575 755 et les nombres avec un ou deux 0: 174 nombres
Vendredi 18 Décembre
Jeanne a une probabilité de gagner de j = 1 / 2
Karim a p = k et Laura p = l avec k + l = 1 / 2 et k = 2 l. Soit k = 1 / 3 et l = 1 / 6.
La probabilité que Jeanne gagne trois manches puis Karim deux puis Laura un est p = j³ × k² × l = 1 / 432
Dans les 6 parties, Jeanne a ${6\choose 3}$ = 20 combinaisons d’en gagner 3. Karim a ${3\choose 2}=3$ possibilités pour gagner 2 des 3 restantes.
Donc p = 20 × 3 × 1 / 432 = 5 / 36
réponse: 5 / 36
Lundi 21 Décembre
Les deux triangles intérieurs de base les côtés inférieu et supérieur ont des aires identiques.
Aire triangle = 3 + 6 + quadrilatère central = 5 + x + quadrilatère central
D’où x = 3 + 6 - 5 = 2
réponse: x = 2
Mardi 22 Décembre
Une personne connait au maximum trois personnes.
Ces trois personnes connaissent à leur tour trois personnes au maxium mais parmi ces trois connaissances il doit y avoir la première personne (connaissance en commun). Donc elles ne peuvent connaitre que deux autres différentes.
Il ne peut y avoir d’autres personnes sinon la première personne n’aurait pas de connaissance en commun avec ces nouvelles.
Soit au total: 1 + 3 + 6 = 10
réponse: 10
Mercredi 23 Décembre
Pythagore donne le résultat immédiatement: AE = √((20 - 15)² + 20²) = √425 = 5 √17
réponse: 5 √17 cm
Jeudi 24 Décembre
Il y a 4 × 5 = 20 nombres pair-impair (le zéro est exclu)
Il y a 5 × 5 = 25 nombres impair-pair
réponse: 55
Vendredi 25 Décembre
20202020 = 10001 × 2020
La moyenne est donc 20202020 / 2020 = 10001
réponse: 10001
Lundi 28 Décembre
p = 13 convient.
p ne peut être multiple de 3 (ni de 2 d’ailleurs). Il s’écrit donc 3k + 1 ou 3k + 2. p-10 et p+10 valent alors:
\[\begin{aligned} &\begin{cases} p-10=(3k+1)-10 = 3k - 9 = 3(k-3) : \text{le nombre est multiple de 3 et donc non premier} \\ p+10=(3k+1)+10 \end{cases} \\ \\ &\begin{cases} p-10=(3k+2)-10 \\ p+10=(3k+2)+10 = 3k + 12 = 3(k+4) : \text{le nombre est multiple de 3 et donc non premier} \end{cases} \end{aligned}\]Donc la seule solution est p = 13.
réponse: p = 13 (3, 13, 23 premiers)
Mardi 29 Décembre
$125000027=5^3\times 100^3+3^3=500^3+3^3$
Or, $a^3+b^3=(a+b)(a^2-ab+b^2)$.
Donc: $125000027=(500+3)(500^2-500\times 3+3^2)$
$125000027=503\times(250000-1500+9)=248509$
Par ailleurs, on peut vérifier que cela correspond à la décomposition en facteurs premiers.
réponse: 503 et 248509
Mercredi 30 Décembre
Tous les nombres premiers 2 3 5 7 11 13 17 19 conviennent par définition.
1 aussi convient à l’énoncé.
réponse: 9
Jeudi 31 Décembre
Les points délimitent des triangles équilatéraux de côté 4 cm. Ainsi il y a un hexagone régulier inscrit dans le cercle, dont le rayon vaut donc le côté de l’hexagone, à savoir 4 cm.
réponse: 4 cm