Calendrier Mathématique Février 2020
Lundi 3 Février
une solution: 1 2 5 6 3 4 7 8 11 9 12 10
Programme en Python pour les chercher toutes. Il y en a 1990656 sur 12! permutations.
#!/usr/bin/env python3
from itertools import permutations
nb = 0
for n in permutations(range(1, 13)):
if n[0] != 1:
# pas la peine de refaire toutes les permutations avec 1 à une autre place
nb *= 12
break
for i in range(12):
a, b, c = n[i], n[(i + 1) % 12], n[(i + 2) % 12]
if (a + b + c) % 3 == 0:
break
else:
print(" ".join(map(str, n)))
nb += 1
print(nb)
réponse: 1 2 5 6 3 4 7 8 11 9 12 10
Mardi 4 Février
L’hexagone est rempli de:
- 7 petits hexagones, eux-mêmes équivalents à 6 petits triangles équivaléraux, soit 42
- 12 petits triangles équilatéraux
L’aire coloriée est constituée de:
- 6 petits triangles
- 1 hexagone, soit 6 petits triangles
La proportion est donc: (6 + 6) / (42 + 12) = 2 / 9
réponse: 2 / 9
Mercredi 5 Février
Programme Python.
#!/usr/bin/env python3
def rev(n):
""" Retourne le nombre n écrit à l'envers dans sa représentaiton décimale. """
u = 0
while n != 0:
n, r = divmod(n, 10)
u = u * 10 + r
return u
print("réponse:", sum(1 for n in range(100, 1000) if rev(n) > n))
réponse: 360
Jeudi 6 Février
- susie < marie
- laurie < lucie
- noémie = rosie
- sophie < susie
- laurie = marie
-
lucie < noémie
- sophie < susie < marie = laurie < lucie < noémie = rosie
réponse: Sophie
Vendredi 7 Février
Programme Python.
#!/usr/bin/env python3
s = 0
for n in range(10, 100):
d, u = divmod(n, 10)
if n + (d + u) ** 2 == u * 10 + d:
print(n)
s += n
print("réponse:", s)
réponse: 27
Lundi 10 Février
La face qui touche les dés 2 et 3 est 1 puisque les 5 autres nombres sont visibles.
Donc la face entre les dés 1 et 2 est 6. Et par conséquant la face cherchée est 1.
réponse: 1
Mardi 11 Février
\[x^2 y^3=6^{12}=2^{12}\times 3^{12}\]Etant entiers, x et y sont donc nécessairement de la forme $2^a\times 3^b$ Il s’agit de résoudre l’équation $2a+3b=12$ avec $(a,b)\in\N$, a étant l’exposant de x et b celui de y. Les solutions sont: (0, 4) (3, 2) (6, 0). Ces solutions sont valables pour les puissances de 2 et de 3. Ce qui fait donc 3 × 3 = 9 solutions.
Recherche exhaustive en Python.
#!/usr/bin/env python3
from itertools import product
r = 6 ** 12
nb = 0
for a, b in product(range(7), repeat=2):
x = 2 ** a * 3 ** b
for c, d in product(range(5), repeat=2):
y = 2 ** c * 3 ** d
if x ** 2 * y ** 3 == r:
nb += 1
print(f"{nb:2} x=2^{a}*3^{b}={x:5} y=2^{c}*3^{d}={y:5}")
print("réponse:", nb)
réponse: 9
Mercredi 12 Février
On va considérer l’inverse des nombres, l’ordre sera inversé.
- 1001/1000 = 1 + 1/1000 = 1 + 2/2000 = 1 + 6/6000
- 2003/2000 = 1 + 3/2000 = 1 + 3/2000 = 1 + 9/6000
- 3005/3000 = 1 + 5/3000 = 1 + 5/3000 = 1 + 10/6000
- etc.
On en déduit que 1001/1000 < 2003/2000 etc.
réponse: 1000/1001 > 2000/2003 > 3000/3005 > 4000/4007 > 5000/5009
Jeudi 13 Février
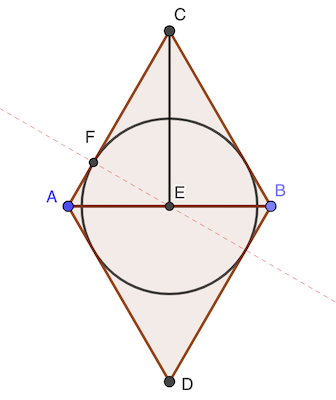
Le centre du cercle est sur la droite AB et le point F est tel que EF est la hauteur issue de E du triangle ACE.
EF × AC = AE × CE
EF × 1 = ½ × √(1 - ½²) = √3 / 4
réponse: √3 / 4 cm
Vendredi 14 Février
√(x - 9) - √(x - 16) = 1
élevons au carré: 2x - 25 - 2 √((x - 9) (x - 16)) = 1
simplifions: x - 13 = √((x - 9) (x - 16))
élevons encore au carré: x² - 26x + 169 = x² - 25x + 144
simplifions: x = 169 - 144
d’où: x = 25
réponse: x = 25
Lundi 17 Février
- Il y a tous les nombres 1xxx, soit 10.
- Il y a tous les nombres 111x avec x≠1, soit 9.
- Il y a tous les nombres 1x11 avec x≠1, soit 9.
- Il y a tous les nombres 11x1 avec x≠1, soit 9.
réponse: 37
Mardi 18 Février
Il y a 3 m par triangle, et un triangle de plus à chaque étage. Le linéaire est donc:
3 × (1 + 2 + 3 + … + n) = 3 n (n + 1) / 2
Résolvons: 3 n (n + 1) / 2 = 100
3n² + 3 n - 200 = 0
La solution positive de l’équation est n ≅ 7.68.
On pourra faire 7 étages au max. Il restera 16 m linéaire d’encre dans le stylo.
réponse: 7
Mercredi 19 Février
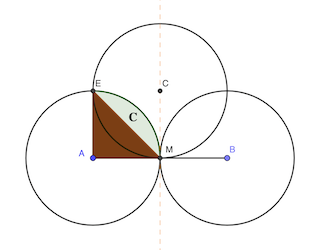
L’aire du secteur de 90° AME est π r² / 4 = π / 4. L’aire du triangle AME est 1 / 2. L’aire du segment circulaire 𝐂 vert est donc π / 4 - 1 / 2.
L’aire coloriée est donc l’aire du cercle moins quatre fois l’aire du segment circulaire. Soit:
π - 4 × (π / 4 - 1 / 2) = 2
réponse: 2 cm²
Jeudi 20 Février
1 + 3 + 5 + … + (2n + 1) = n² = 44100
D’où n = 210. Il y a 210 piles ( 421 pièces dans la plus grande).
1 + 2 + 3 + … + m = 210 où m = nombre d’officiers récompensés.
m (m + 1) / 2 = 210 ⇔ m² + m - 420 = 0 ⇔ m = 20 ou m = -21
réponse: 20 officiers
Vendredi 21 Février
Huit tirages, parce qu’il peut tirer les trois jaunes et quatre bleus en premier. Le tirage suivant sera forcément d’une troisième couleur.
réponse: huit
Lundi 24 Février
Le triangle AMD est exactement le quart du carré.
réponse: 16 m²
Mardi 25 Février
2 et 3 disent la même chose, comme il y a deux inscriptions vraies ça ne peut être que celles-là. Donc 1 est fausse. Et comme le trésor n’est pas dans 2 ni dans 1, il est dans 3
réponse: coffre 3
Mercredi 26 Février
6 kg de pomme coûtent 6 × 3.3 = 19.8 €. Si on rajoute X kg de poire, son mélange coûtera au kg (19.8 + X × 2.5) / (6 + X).
(19.8 + X × 2.5) / (6 + X) = 3.1 ⇒ 19.8 + 2.5 X = 3.1 X + 18.6 ⇒ 1.2 = 0.6 X ⇒ X = 2
Il doit ajouter 2 kg de poire aux 6 kg de pommme pour faire des paniers à 3.1 kg / €.
réponse: 2 kg
Jeudi 27 Février
- 50 mois = 4 ans et 2 mois, soit 4 ans et 8 semaines
- 50 semaines
- 50 jours = 7 semaines et 1 jour
Anne a donc (à quelques jours près) 50 ans + 4 ans + (8 + 50 + 7) semaines + 1 jour, soit 54 + 65 semaines et 1 jour, ou encore 55 ans et 13 semaines. Son prochain anniversaire est celui des 56 ans.
réponse: 56 ans
Vendredi 28 Février
Soit O le centre du pentagone.
L’angle ∠DOE vaut 360 / 5 = 72°. Comme DOE est un triangle isocèle en O, les angles ∠DEO et ∠ODE valent tous les deux (180 - 72) / 2 = 54°.
La somme des angles en E vaut 360° : ∠AEO + ∠OED + ∠DEG = 360 - ∠AEG.
D’où: ∠AEG = 360 - 54 - 54 - 90 = 162°
Comme ∠AEG est isocèle en A (AE = EG), on a ∠GAE = (180 - ∠AEG) / 2 = (180 - 162) / 2 = 9°
réponse: 9°