Calendrier Mathématique Juillet 2020
Mercredi 1 Juillet
Il faut arriver à 9 + 9 + 5 + 1 = 24 soit 6 jetons par pile
| tas 1 | tas 2 | tas 3 | tas 4 | |
|---|---|---|---|---|
| Départ | 9 | 9 | 5 | 1 |
| Mouvement 1 | 8 > | 8 > | 4 > | > 4 |
| Mouvement 2 | 7 > | 7 > | 3 > | > 7 |
| Mouvement 3 | 6 > | 6 > | > 3 | 7 > |
réponse: oui
Jeudi 2 Juillet
- (a²+b²+c²) - (a+b+c)² = -2 a b - 2 a c - 2 b c = 0
⇒ a b + a c + b c = 0
- (a²+b²+c²)(a+b+c) - (a³+b³+c³) = 0
= a² b + a² c + a b² + b² c + a c² + b c²
= a (ab+ac) + b(ab+bc) + c (ac+bc)
= a (-bc) + b (-ac) + c (-ab) = - 3abc
Donc abc = 0. Ce qui signifie que a ou b ou c vaut 0, ainsi qu’une autre et la dernière 1.
réponse: abc = 0
Vendredi 3 Juillet
IJKL couvre le quart de ABCD, puisque IL = 1/2 AD etc.
réponse: 4
Lundi 6 Juillet
La n-ième ligne commence par n(n - 1) + 1.
Ainsi la 21ème ligne commence par 421 et la 20ème finit par 419 donc.
∑ n (impairs ≤ 419) = ∑ n (n ≤ 419) - 2∑n (n ≤ 214) = 419 × 420 / 2 + 2 × 209 × 210 / 2 = 44100
réponse: 44100
Mardi 7 Juillet
| déclaration | il pleut | il fait beau |
|---|---|---|
| ① aujourd’hui il pleut | tortue | serpent |
| ② celui qui vient de parler ment | serpent, renard | tortue |
| ③ aujourd’hui il fait beau | renard | tortue |
| ④ celui qui vient de parler ment ou je suis un renard | tortue, serpent | renard |
réponse: 2
Mercredi 8 Juillet
ACE est un triangle équilatéral.
ABC doit être un triangle rectangle d’hypothénuse √85. Les deux autres côtés mesurent donc 2 et 9 car 2² + 9² = 85.
CDE doit être aussi un triangle rectangle d’hypothénuse √85. L’autre possibilité est 6² + 7² = 85.
Il faut minimiser AFE. Comme 9 < √85 < 10 et que AF et FE doivent être entiers, la plus petite distance est 10 (1+9, 2+8, etc). Mais 2,6,7,9 sont déjà utilisés. Il faut choisir 8+3=11 au minimum.
Le périmètre est donc 11 + 13 + 11 = 35
réponse: 35
Jeudi 9 Juillet
a × b = a + b
(a - 1) × (b - 1) = a × b - a - b + 1 = 1
L’équation (a - 1) × (b - 1) = 1 admet deux solutions entières: (0, 0) et (2, 2)
réponse: (0, 0) et (2, 2)
Vendredi 10 Juillet
Soit s(a) = a (a + 1) / 2 la somme des entiers de 1 à a
f(a,b) = s(b) - s(a - 1)
f(133, 533) = 533 × 534 / 2 - 132 × 133 / 2 = 133533
réponse: 133533
Lundi 13 Juillet
Le carré d’un nombre impair (2k+1) est impair et vaut 1 (mod 4). En effet:
(2k + 1)² = 4k² + 4k + 1 = 1 (mod 4)
Or 2019 = 2016 + 3, donc 2019 (mod 4) = 3.
Donc tout nombre que se termine par 2019 ne peut être être le carré d’un entier. Et même tout nombre qui se termine par 19.
Le code Python suivant permet de lister les terminaisons à 2 chiffres des carrés d’entier:
set((k*k)%100 for k in range(0,100))
réponse: non - aucun carré d’entier se termine par 2019
Mardi 14 Juillet
Il y a :
- 12 carrés 1×1
- 5 carrés 2×2
- 8 rectangles 1×2
- 8 rectangles 2×1
- 4 rectangles 1×3
- 4 rectangles 3×1
- 2 rectangles 1×4
- 2 rectangles 4×1
- 2 rectangles 2×3
- 2 rectangles 3×2
- 1 rectangle 2×4
- 1 rectangle 4×2
réponse: 17 carrés, 34 rectangles, 51 en tout
Mercredi 15 Juillet
2a⁴ - 4ab + b² + 2 = 0
2a⁴ - 4a² + 4a² - 4ab + b² + 2 = 0
2a⁴ - 4a² + (2a - b)² + 2 = 0
Il faut que a soit au moins solution de l’inéquation suivante pour que celle ci-dessus ait une chance d’être vérifiée puisque le seul terme négatif est -4a².
2a⁴ - 4a² + 2 ≤ 0
a² = 1
- a² = 1 ⇒ 2 ± 4b + b² + 2 = 0 ⇒ (± b - 2)² = 0 ⇒ b = ± 2
réponse: les solutions sont (-1, -2) (1, 2)
Jeudi 16 Juillet
2 -A→ 1 / 2 -B→ 1 -A→ 1 -B→ 2
La séquence ABAB est invariante pour l’entrée. 2020 = 505 × 4, donc le résultat est 2.
réponse: 2
Vendredi 17 Juillet
Soient vₐ et vᵩ la vitesse en nombre de pas d’Abdoul et de son fils, 𝑥 = nombre de pas d’Abdoul
- vₐ = 6
- vᵩ = 3 / 5 × 7 = 4.2
Leurs positions respectives sont données par :
- pₐ = vₐ × (𝑥 - 3 / 5 × 30)
- pᵩ = vᵩ × 𝑥
En posant pₐ = pᵩ, on obtient:
6 × (𝑥 - 3 / 5 × 30) = 4.2 𝑥
1.8 × 𝑥 = 6 × 18 = 108
𝑥 = 108 / 1.8 = 60
réponse: 60 pas
Lundi 20 Juillet
aire ABC = 1 / 2 m²
aire CDE = 3 / 4 × 1 / 2 = 3 / 8 = CD² / 2
d’où CD = √3 / 2
réponse: √3 / 2 cm
Mardi 21 Juillet
Il faut trouver le multiple du ppcm de (2, 3, 4, 5, 6) + 1 qui soit un multiple de 7.
ppcm = 3 × 4 × 5 = 30
En tâtonnant, on trouve 301.
Vérification en Python:
for i in (2, 3, 4, 5, 6, 7): print(i, "->", 301 % i)
réponse: 301
Mercredi 22 Juillet
Les candidats sont nécessairement un carré, soit 1, 4, 9, 16, etc.
1 et 9 conviennent car:
- 1 a un diviseur (1) et 1 = 1²
- 9 a trois diviseurs (1 3 9) et 9 = 3²
Si n² avec n premier, il a trois diviseurs. Seul 9 convient.
Si n² avec n puissance d’un premier, il a (1 + k) diviseurs. (1 + k) = p^k. Seul k = 0 convient.
Sinon n² est a plusieurs facteurs premiers, et son nombre de diviseurs est ∏(1 + k) et ça revient au problème précédent.
Programme Python de recherche.
#!/usr/bin/env python3
import math
def divisors(n):
divs = [1, n]
for i in range(2, int(math.sqrt(n)) + 1):
q, r = divmod(n, i)
if r == 0:
divs.extend([i, q])
return list(sorted(set(divs)))
for n in range(1, 101):
if n == len(divisors(n)) ** 2:
print(n)
réponse: deux nombres (1 et 9)
Jeudi 23 Juillet
k = 120 / (4 + 7 + 9) = 6
réponse: Mélissa reçoit 42 cerises
Vendredi 24 Juillet
a × b = 8
p = 2 (a + b) = 2 (a + 8 / a)
p’ = 2 - 16 / a²
Le minimum est atteint pour 2 - 16 / a² = 0 soit a = 2 √2, ce qui correspond au carré.
La diagonale du carré fait 2√2 × √2 = 4
réponse: 4 m
Lundi 27 Juillet
On a d > 0 donc 1 / d < 1. Puis c + 1 / d > 1, donc 1 / (c + 1 / d) < 1, et ainsi de suite.
42 / 11 = a + 1 / x avec x > 1. Donc a = ⌊42 / 11⌋ = 3.
42 / 11 - 3 = 9 / 11. Donc 11 / 9 = b + 1 / y. D’où b = 1.
On peut calculer c: 11 / 9 - 1 = 2 / 9. D’où c = ⌊9 / 2⌋ = 4.
Et enfin, d = 1 / (9 / 2 - 4) = 2
Vérification avec PARI/GP, SageCell, etc.
a=3; b=1; c=4; d=2
1/(a+1/(b+1/(c+1/d))) - 11/42
réponse: a + b + c + d = 3 + 1 + 4 + 2 = 10
Mardi 28 Juillet
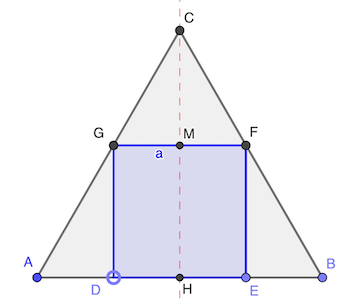
Comme CFG est nécessairement équilatéral, FG = CG = CF = a.
GCM est rectangle en M et GM = 1 / 2 a. D’où CM = a √3 / 2
CH = CM + HM = a (1 + √3 / 2)
CH = √3 / 2 AB = √3 / 2
D’où a = √3 / (2 + √3)
réponse: √3 / (2 + √3) m
Mercredi 29 Juillet
La somme des trois plus petits est (n-1) + n + (n + 1) = 3n. Donc n = 11.
Les nombres sont: 10 11 12 13 14 15 16.
La somme des trois plus grands est donc 45.
réponse: 45
Jeudi 30 Juillet
Il faut que 1 ≤ n ≤ 30 (sinon 2n > n + 30 et criète impossible).
Il faut que n soit pair mais pas multiple de 4 (à cause du n + 30).
En testant les nombres 2, 6, … 30 on trouve que 2 6 10 30 conviennent mais pas les autres.
réponse: quatre (2 6 10 30)
Vendredi 31 Juillet
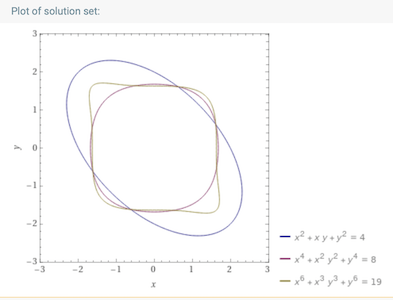
① x² + xy + y² = (x + y)² - xy = 4
② x⁴ + (xy)² + y⁴ = (x² + y²)² - (xy)² = (4 - xy)² - (xy)² = 8
16 - 8xy = 8
xy = 1
③ x⁶ + (xy)³ + y⁶
Utilisons WolframAlpha pour le calcul symbolique:
① × ② - ③ = 4 × 8 - ③ = xy (x⁴ + y⁴) + 2 (xy)² (x² + y²)
= xy (8 - (xy)²) + 2 (xy)² (4 - xy)
= 1 × (8 - 1) + 2 × 1 × (4 - 1) = 7 + 6 = 13
D’où: ③ = 4 × 8 - 13 = 19
réponse: 19