Calendrier Mathématique Mai 2020
Vendredi 1 Mai
La mise en équation donne: 4 / 5 n + 4 / 5 = n
Soit n - 4 / 5 n = 4 / 5
D’où n = 4
réponse: quatre chats
Lundi 4 Mai
Soit a,b,c les dimensions de la cage. On a:
- x = ab ①
- y / 5 = ac ⇔ y = 5ac ②
- 5xy = bc ③
En remplaçant dans ③ x et y tels que donnés par ① et ②:
5 ab × 5 ac = bc
D’où a = 1 / 5
Le volume de la cage est abc.
abc = bc / 5 = xy
réponse: xy
Mardi 5 Mai
Recherche avec programme Python.
#!/usr/bin/env python3
import math
def divisors(n):
divs = [1, n]
for i in range(2, int(math.sqrt(n)) + 1):
q, r = divmod(n, i)
if r == 0:
divs.extend([i, q])
return list(sorted(set(divs)))
n = 2
while True:
u = [0] * 10
nu = 0
for d in divisors(n):
if u[d % 10] == 0:
u[d % 10] = 1
nu += 1
if nu == 10:
print(n, divisors(n))
exit()
n += 1
réponse: 270
Mercredi 6 Mai
En triant selon l’énoncé, on obtient:
marie < sylvie < sophie < ana < elsa < pauline
Marie a 15€, Sylvie 30€, Sophie 45€, etc.
réponse: Sophie 45€
Jeudi 7 Mai
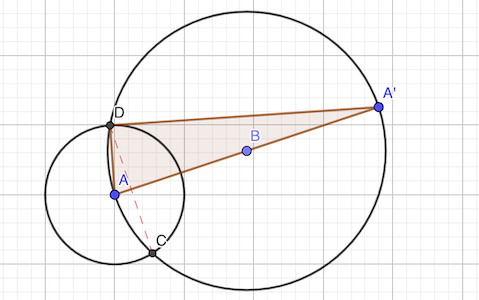
ADA’ et ACA’ sont deux triangles rectangles dont deux côtés ont pour longueur 1 et 4 (hypoténuse), d’où le troisième côté AA’ = √(4² - 1) = √15
La distance DC recherchée est le double de la hauteur 𝒉 des triangles. On peut écrire (calcul de l’aire de deux façons différentes):
AD × DA’ = 𝒉 × AA’
Soit DC = 2 𝒉 = AD × DA’ / AA’ × 2 = 1 × V15 / 4 × 2 = V15 / 2
réponse: V15 / 2 cm
Vendredi 8 Mai
Mise en équation (V volume de la piscine, Tᵢ le débit par jour du tuyau 𝑖):
- V = (T₁ + T₂) × 3
- V = (T₂ + T₃) × 4
- V = (T₁ + T₃) × 6
4V + 3V + 2V = 9V = 12 (T₁ + T₂) + 12 (T₂ + T₃) + 12 (T₁ + T₃) = 24 (T₁ + T₂ + T₃)
D’où V = 8 / 3 (T₁ + T₂ + T₃)
réponse: 64h ou 2 jours et 16h
Lundi 11 Mai
On pose la division 469 / 1998:
- 469 * 10 / 1998 = 2 + 694 / 1998
- 694 * 10 / 1998 = 3 + 946 / 1998
- 946 * 10 / 1998 = 4 + 1468 / 1998
- 1468 * 10 / 1998 = 7 + 694 / 1998
On retrouve le reste 694 donc les décimales 347 vont se répéter à l’infini.
469 / 1998 = 0.2347347347…
Le premier chiffre est 2, les 3k+2 des 3, 3k+3 des 4 et 3k+4 des 7.
Comme 2020 = 672 * 3 + 4, le 2020e chiffre est un 7.
réponse: 7
Mardi 12 Mai
- N = n²
- N + 3333 = m²
- n² + 3333 = m²
- (m - n)(m + n) = 3333 = 3 × 11 × 101
m - n = 3 et m + n = 1111 ⇒ 2n = 1114 ⇒ n = 554 ❌ n doit être inférieur à 100 pour que n² soit inférieur à 10000
m - n = 33 et m + n = 101 ⇒ 2n = 68 ⇒ n = 34, n² = 1156 ✅
réponse: 34
Mercredi 13 Mai
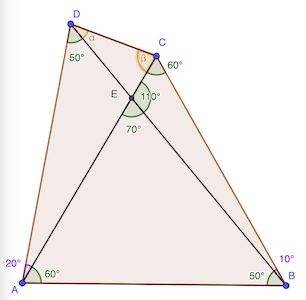
Du fait des angles:
- le triangle ABC est équilatéral, donc AB = AC = BC
- le triangle ABD est isocèle en A, donc AB = AD
Ainsi ACD est également isocèle car AC = AD.
20° + 2 β = 180°
D’où β = 80°
réponse: 80°
Jeudi 14 Mai
On factorise l’équation:
a³ + b³ - 2a²b - 2ab² = 0
a³ + b³ - 2a²b - 2ab² + 5 a²b + 5 ab² = 5 (a²b + ab²)
(a + b)³ = 5ab (a + b)
On peut simplifier puisque a et b sont strictement positifs, donc a + b non nul.
(a + b)² = 5ab
a² + b² + 2ab = 5ab
D’où:
a² + b² = 3ab ①
En disisant par b² puis a², on a les équations suivantes:
- a² / b² + 1 = 3 a / b
- 1 + b² / a² = 3 b / a
Additionnées, cela donne:
a² / b² + b² / a² = 3 a / b + 3 b / a - 2 = 3 (a² + b²) / ab - 2
Or, on sait que (a² + b²) / ab = 3 ①
Donc: a² / b² + b² / a² = 3 × 3 - 2 = 7
réponse: a² / b² + b² / a² = 7
Vendredi 15 Mai
Pour 3a + b +c, il suffit b + c soit multiple de 3.
Supposons d’abord que b < c
- 0-3 0-6 0-9
- 1-2 1-5 1-8
- 2-4 2-7
- 3-6 3-9
- 4-5 4-8
- 5-7
- 6-9
- 7-8
Ce qui donne 15 possibilités. Soit 30 en considérant b > c. Il faut rajouter les 4 cas où b = c: 0-0 3-3 et 6-6 9-9.
Soit 34 possibilités, qu’il faut multiplier par 9, le nombre de valeurs que peut prendre a.
réponse: 306
Lundi 18 Mai
Le petit carré central ne bouge pas: s’il est blanc il restera blanc. Il faut donc qu’il soit noir dès le début. Probabilité = 1 / 2.
Pour qu’un petit carré sur le bord ne devienne pas noir il faut que son antécédent dans la rotation soit également blanc.
| BBNN | BBBN | BBBB | NBBN | NBBB | NNBB | BNNB | BBNB | BNBB |
|---|---|---|---|---|---|---|---|---|
·B· |
·B· |
·B· |
·N· |
·N· |
·N· |
·B· |
·B· |
·B· |
N·B |
N·B |
B·B |
N·B |
B·B |
B·N |
B·N |
B·B |
B·N |
·N· |
·B· |
·B· |
·B· |
·B· |
·B· |
·N· |
·N· |
·B· |
Sur les 2⁴ = 16 possibles, Il y a donc 9 dispositions dans lequelles deux blancs au moins sont successifs.
Il y a donc 7 dispositions convenables.
Cela vaut pour les petits carrés au milieu et pour ceux aux sommets.
En tout il y a: 1 / 2 × 7 / 16 × 7 / 16 = 49 / 512
réponse: 49 / 512
Mardi 19 Mai
Les droites confondues sont celles qui ont une même pente, i.e. s’il existe k entier > 1 tel que xk = y ou yk = x, ou autrement dit si x et y ne sont pas premiers entre eux.
Comptage avec programme Python.
#!/usr/bin/env python3
from fractions import Fraction
from math import gcd
n = 0
u = set()
for x in range(1, 11):
for y in range(1, 11):
# détermination: x et y premiers entre eux
if gcd(x, y) == 1:
n += 1
# détermination: pente unique
a = Fraction(y, x)
u.add(a)
print("réponse:", n, len(u))
réponse: 63
Mercredi 20 Mai
Soit C le nombre placé dans le rond central. En additionnant les sommes des 5 droites, on a:
5 × 18 = 1 + 2 + … + 11 + 5 × C - C
Soit, 90 = 66 + 4 × C
D’où C = 6
réponse: 1-6-11 2-6-10 3-6-9 4-6-8 5-6-7
Jeudi 21 Mai
𝑥 ne peut être entier puisque 17 n’est pas un carré. Le carré strictement inférieur est 16. Donc
𝑥 = (17 - 16) / √16 + √16 = 4.25
réponse: 𝑥 = 4.25
Vendredi 22 Mai
⚠️ 🤪 Il manque une précision essentielle dans l’énoncé: le triangle est supposé équilatéral ! 🤪
Le rapport est alors 4 / 3.
Si le triangle est quelconque, il y a une infinité de réponses…
réponse: 4 / 3 ⚠️
Lundi 25 Mai
Comptage avec programme Python.
#!/usr/bin/env python3
from itertools import product
n = sum(1 for a, b, c in product(range(0, 10), repeat=3) if a + b + c == 10)
print("réponse:", n)
réponse: 63
Mardi 26 Mai
Les carrés entre 11 et 109 sont: 16 25 36 49 64 81 100
réponse: 7
Mercredi 27 Mai
Soit n l’agent de Nico et l celui de Léa.
n + l = 80
Echange 1:
- n’ = n - l
- l’ = 2 l
Echange 2:
- n” = (n - l) * 2
- l” = 2l - (n - l)
Echange 3:
- n”’ = (n - l) * 2 - [ 2l - (n - l) ] = 0
- l”’ = (n - l) + (n - l) * 2 = 80
2n - 2l - 2l + n - l = 3n - 5l = 0
Soit 3n = 5l.
n + 3 / 5 n = 8 / 5 n = 80
Nico avait 50€
réponse: 50€
Jeudi 28 Mai
On trace la hauteur AH de ABC. Soit H’ l’intersection avec B’C’. AH’ est aussi hauteur de AB’C’ (car ⟂).
La hauteur AH de ABC est 3 × 4 / √(3² + 4²) = 12 / 5 (aire du triangle).
Le théorème de Thalès donne:
AB’ / AB = AH’ / AH = AC’ / AC
Soit AB’ = 3 × (12 / 5 - 1) / (12 / 5) = 7 / 4
et AC’ = 4 × (12 / 5 - 1) / (12 / 5) = 7 / 3
L’aire de AB’C’ est donc: 7 / 4 × 7 / 3 / 2 = 49 / 24 m²
réponse: 49 / 24 m²
Vendredi 29 Mai
Il faut chercher les entiers a < 1000 qui vérifient:
1000 a + 154 = 154 k ⇔ 500 a = 77 (k - 1) avec k ∈ 𝐍
Comme 500 et 77 sont premiers entre eux, ce sont donc tous les multiples de 77 entre 100 et 1000.
Il y en a ⌊ 900 / 77 ⌋ = 11
Vérification en Python:
sum(1 for n in range(100000, 1000000) if n % 154 == 0 and n % 1000 == 154)
réponse: 11