Calendrier Mathématique Décembre 2021

Solutions 2021 - Homepage

Mercredi 1 Décembre

• 9 chiffres de 1 à 9
• 2 × 90 chiffres de 10 à 99
• 3 × 900 chiffres de 100 à 999
• 4 × 1022 chiffres de 1000 à 2021

Soit 9 + 2 × 90 + 3 × 900 + 4 × 1022 = 6977

Vérification en Python:

len("".join(map(str, range(1, 2022))))

réponse: 6977

Jeudi 2 Décembre

Il n’y a que deux possibilités de suites sans nombres consécutifs à côté.

• 1 3 5 2 4
• 1 4 2 5 3

Elles correspondent d’ailleurs, au sens de rotation près.

Il y a donc 2 × 5 solutions.

Vérification avec programme Python.

#!/usr/bin/env python3

import itertools

n = 0
for p in itertools.permutations("12345"):
    pp = "".join(p)  # recrée une chaine
    pp = pp + pp  # pour éliminer si le premier et le dernier sont consécutifs
    if "12" in pp or "23" in pp or "34" in pp or "45" in pp:
        continue
    if "21" in pp or "32" in pp or "43" in pp or "54" in pp:
        continue
    print("".join(p))
    n += 1
print("réponse:", n)

réponse: 10

Vendredi 3 Décembre

On a:

37² = AC² + AB²

AD² + AC² = CD² ⇒ AC² = 13² - 5² = 144 ⇒ AC = 12 cm

AB² = 37² - 144 = 1225

D’où AB = 35 cm et l’aire 35 × 12 / 2 = 210 cm²

réponse: 210 cm²

Lundi 6 Décembre

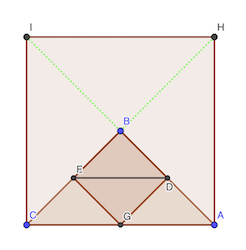
L’aire du triangle ABC est 8 cm². Les aires des petits triangles BED etc. est 2 cm². En effet E est le milieu de BC, G le milieu de CA et D le milieu de AD. Donc l’aire du trapèze est 6 cm².

réponse: 6 cm²

Mardi 7 Décembre

3n+2 est toujours impair. Donc les nombres à considérer doivent être impairs. De plus, ça ne peut pas être un multiple de 3 car 3n+2 n’est pas divisible par 3.

En carré impair entre 5 et 302 sans facteur 3, il y a 25 49 169 289.

• 25 - 2 = 22 pas divisible par 3 et pas ok
• 49 - 2 = 47 idem
• 169 - 2 = 167 idem
• 289 - 2 = 287 idem

réponse: aucun

Mercredi 8 Décembre

Autant compter avec un programme.

#!/usr/bin/env python3

import itertools
from sympy.ntheory import sieve

primes = sieve._list

n = 0
for p in itertools.permutations([2, 4, 6, 8]):
    for a, b in zip([1, 3, 5, 7], p):
        if a + b not in primes:
            break
    else:
        print(p)

réponse: 6

Jeudi 9 Décembre

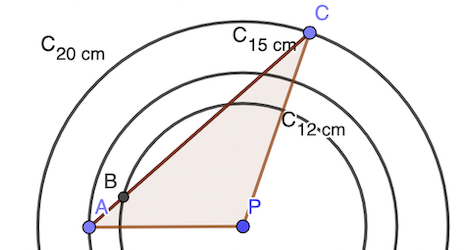
On va essayer de maximiser l’aire du triangle APC.

Aire = AP × h / 2 avec h la hauteur issue de C. La valeur est maximale quand h = AC, qui est la plus grande valeur. Elle a pour valeur 20 × 15 / 2 = 150 cm².

Reste à vérifier si B est sur le cercle de 12 cm lorsque AP et AC sont perpendiculaires.

AC = √(AP² + AC²) = √(225 + 400) = √625 = 25.

La hauteur issue de P doit vérifier h × 25 / 2 = 150 pour que le calcul de l’aire soit correct. On trouve h = 12 cm. Donc AC coupe bien le cercle de 12 cm en un point P. De plus, B est tangent au cercle.

réponse: 150 cm²

Vendredi 10 Décembre

Soit a et p les âges de Arlette et Patrick en 2021.

• p - 3 = 3 (a - 3) / 4 ⇒ 4p = 3a + 3 ①
• p + 3 = a - p + 20 ⇒ 2p = a + 17 ②

① - 2 × ② ⇒ a + 3 - 34 = 0, soit a = 31

réponse: 31 ans

Lundi 13 Décembre

(√a + √b)² = (√c)²

a + 2 √ab + b = c

Cela implique que √ab doit être un entier. C’est possible avec notamment a = pⁿ et b = pⁿ⁺² : ab = p²ⁿ⁺² et √ab = pⁿ⁺¹

réponse: oui

Mardi 14 Décembre

La première ligne a pour somme minimale 17 + 1 + 2 = 20. Les deux cases de la dernière doivent être remplies par 7 et 8. Si somme de la première ligne est supérieure à 20, la dernière ne pourra pas être remplie.

La troisième ligne doit ajouter 11, et une seule possibilité: 5 + 6.

La deuxième ligne: 13 + 3 + 4 = 20 : ça fonctionne.

Il y a un seul choix par ligne. 2⁴ = 16 choix si on tient compte de l’ordre.

réponse: 16

Mercredi 15 Décembre

Il y a n² lancés possibles. Le nombre de couples de nombres consécutifs est (n - 1) si le premier est plus petit et (n - 1) s’il est plus grand. On donc résoudre l’équation:

2(n - 1) / n² = 7 / 32

Cette équation admet deux solutions: 8 / 7 et 8. Comme n doit être entier, n = 8.

réponse: 8

Jeudi 16 Décembre

Ecrivons le système de quatre équations à quatre inconnus:

camille + sasha + fille + fils = 85 ①
fille = fils + 5 ②
camille = sasha + 2 ③
sasha + 2 = 3 (fille + 2) ④

① avec ② et ③ : (sasha + 2) + sasha + (fils + 5) + fils = 85 ⇒ sasha + fils = (85 - 5 - 2) / 2 = 39 ⑤ ④ : sasha + 2 = 3 ((fils + 5) + 2) ⇒ sasha - 3 fils = 21 - 2 = 19 ⑥

⑤ - ⑥ fils + 3 fils = 39 - 19 = 20 ⇒ fils = 5

On complète:

• fille = 5 + 5 = 10
• sasha = 3 × (10 + 2) - 2 = 34
• camille = 34 + 2 = 36

réponse: camille=36 sasha=34 fille=10 fils=5

Vendredi 17 Décembre

Les nombres candidats se terminent par 2 4 6 8 (divisibles par 4 et pas par 5). Et commmencent par 5 (inverse divisible par 5 et pas par 4).

Dans cette plage, seuls 52 et 56 conviennent (sinon pas de divibilité par 4).

réponse: 52 et 56

Lundi 20 Décembre

Ahmed tire :

• 1: aucune possibilité
• 2: aucune possibilité
• 3: Bernard doit faire un double 1 : 1 / 36
• 4: Bernard doit faire 1-1 1-2 : 3 / 36
• 5: Bernard doit faire 1-1 1-2 2-2 1-3 : 6 / 36
• 6: Bernard doit faire 1-1 1-2 2-2 1-3 1-4 2-3 : 10 / 36

Soit en tout 1 + 3 + 6 + 10 = 20 sur les 6³ tirages possibles = 20 / 216 = 5 / 54

Programme Python de vérification.

#!/usr/bin/env python3

n = 0
for a in range(1, 7):
    for b1 in range(1, 7):
        for b2 in range(1, 7):
            if a > b1 + b2:
                # print(a,b1,b2)
                n += 1

print("réponse:", n, "/ 216")

réponse: 5 / 54

Mardi 21 Décembre

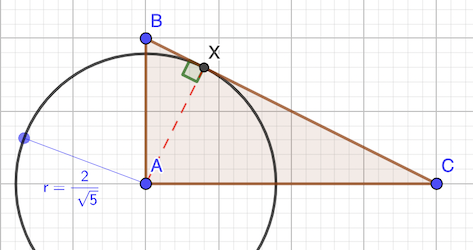
aire ABC = 1 × 2 / 2 = 1 cm²

BC = √(1 + 2²) = √5 cm

Soit AH la hauteur issue de A, H ∈ (BC). On a AH × BC / 2 = aire ABC = 1 cm².

D’où AH = 1 × 2 / BC = 2 / √5 cm. H est X sont donc confondus et il n’y a pas d’autre point X possible.

Ainsi, AX est la hauteur issue de A et donc AX est perpendiculaire à BC.

réponse: 90°

Mercredi 22 Décembre

Si a et b sont solutions de l’équation x² + ax + b = 0, on a:

• a² + a × a + b = 0 ⇒ 2a² + b = 0 ①
• b² + a × b + b = 0 ⇒ a + b + 1 = 0 (b ≠ 0) ②

On en tire:

• ① - ② ⇒ 2a² - a - 1 = 0 ⇒ a = 1 ou - 1 / 2
• ② ⇒ b = -1 - a = -2 ou -1 / 2

On peut calculer les deux valeurs possibles de a - b:

• a - b = 1 - (-2) = 3
• a - b = -1 / 2 - (-1 / 2) = 0 : non valide car a ≠ b (énoncé)

réponse: 3

Jeudi 23 Décembre

• Etape 0: 7
• Etape 1: (7 - 1) + 7 = 13
• Etape 2: (13 - 1) + 7 = 19

Suite uₒ = 7 uₙ = uₙ₋₁ + 6

uₙ = = n × 6 + 7

uₙ > 2021 ⇔ n × 6 + 7 > 2021 ⇔ n > 2014 / 6 ⇒ n > 335 et donc uₙ = 336 * 6 + 7 = 2023

réponse: 2023

Vendredi 24 Décembre

La somme de la ligne 4 est 14 et celle de la première 11. Si on supprime un nombre de la première la somme sera au maximum 10. Or, dans la dernière il faut supprimer 4 ou 7 si on veut une somme inférieure à 11.

Si on enlève 7, la somme à atteindre sera 7. Ce qui n’est pas possible avec la première ligne puisqu’on peut faire 6, 8, 9 ou 10.

Il faut donc enlève 4 à la dernière et la somme à atteindre est 10. Le tableau s’en suit.

réponse: somme = 10

2 * 5 3
3 4 3 *
1 3 * 6
* 2 1 7

Lundi 27 Décembre

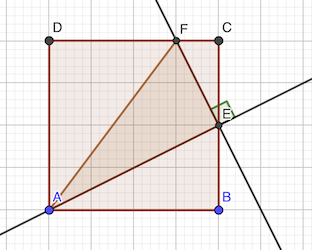
Les triangles ABE et CEF sont semblables (mêms angles).

Donc CF / CE = EB / AB = EF / AE = 1 / 2.

AE = √(2² + 4²) = √20 = 2√5

On en ddéuit que EF = V5

L’aire du triangle AEF est donc AE × EF / 2 = 2√5 × √5 / 2 = 5

réponse: 5 cm²

Mardi 28 Décembre

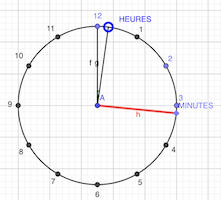
Soit t le temps en secondes.

Les angles des heures et minutes sont donnés par les formules suivantes:

• h = ((t / 3600) * (360 / 12)) mod 360 = (t / 120) mod 360
• m = ((t / 60) * (360 / 60)) mod 360 = (t / 10) mod 360

La relation d’angle est: m = 12 × h

Il faut résoudre m - h = 90 + 180 × k, soit 11 × h = 90 + 180 × k

En 12h, les aiguilles seront perpendiculaires 22 fois. En 24h, le double.

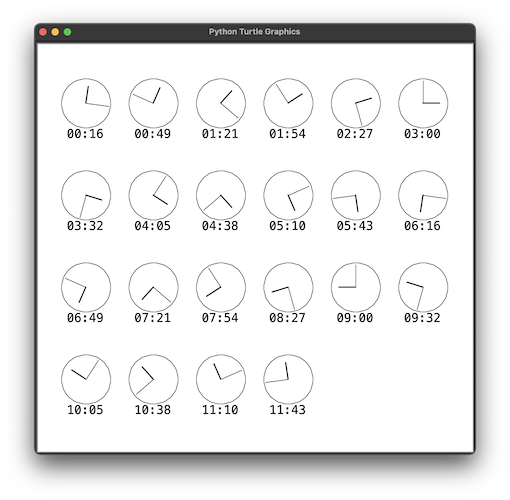
programme de calcul programme de dessin

réponse: 44

Mercredi 29 Décembre

Soit a et n entiers.

√a - √2021 = √n

a + 2021 - 2√(a 2021) = n

2021 = 43 × 47

Donc a doit être de la forme 43 × 47 × k² pour que √(a 2021) soit entier.

• Si k = 1, √a - √2021 = 0 ❌
• Si k = 2, 2√2021 - √2021 = 1 ✅

réponse: 8084

Jeudi 30 Décembre

Il y a 7! = 5040 façons de disposer les nombres 1 à 7.

Il y a 3! = 6 façons de disposer les nombres 1 à 3.

Ainsi parmi les 5040 permutations, il y en a une sur six dans laquelle 1 2 3 sont dans cet ordre.

5040 / 6 = 840

Programme Python de vérification.

#!/usr/bin/env python3

from itertools import permutations

n = 0
for perm in permutations(range(1, 8)):
    prev = 0
    for i in perm:
        if i == 1 and prev == 0:
            prev = 1
        elif i == 2 and prev == 1:
            prev = 2
        elif i == 3 and prev == 2:
            n += 1
            break

print("réponse:", n)

réponse: 840

Vendredi 31 Décembre

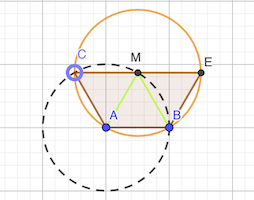
Le quadrilatère doit être inscriptible. Donc les angles opposés sont supplémentaires. De plus, les triangles ACM et BEM sont isocèles du fait de la longueur de leurs côtés.

L’aire du quadrilatère vaut inscriptible:

A = √((s - a) (s - b) (s - c) (s - d)) avec s = (a + b + c + d) / 2

s = (1 + 1 + 1 + 2)/ 2 = 5 / 2

A = √((5 / 2 - 1)³ (5 / 2 - 2)) = √(27 / 16) = 3 / 4 √3

On a aussi A = 1 / 2 (bc + ad) sin 𝛄 = 3 / 2 sin 𝛄 avec 𝛄 = angle entre les côtés b et c

3 / 2 sin 𝛄 = 3 / 4 √3

sin 𝛄 = √3 / 2

𝛄 = 60° ou 120°

Donc on trouve que les angles du quadrilatère sont 60° ou 120°, que les triangles ACM et BEM sont équilatéraux et donc M le centre du cercle.

réponse: 2 cm