Calendrier Mathématique Février 2021
Lundi 1 Février
Cf. programme en Python.
#!/usr/bin/env python3
# tous les diviseurs qui sont inférieurs à 100
m = max(d for d in range(1, 1260 // 2 + 1) if 1260 % d == 0 and d < 100)
print("réponse:", m)
réponse: 90
Mardi 2 Février
Mise en équation sous forme d’équations linéaires:
| filles | garçons | cheveux_clairs | cheveux_foncés | filles_cheveux_clairs | filles_cheveux_foncés | garçons_cheveux_clairs | garçons_cheveux_foncés | valeurs | |
|---|---|---|---|---|---|---|---|---|---|
| filles=garçons | 1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 40% foncés | 0,4 | 0,4 | 0 | -1 | 0 | 0 | 0 | 0 | 0 |
| 60% clairs | 0,6 | 0,6 | -1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 75% foncés=filles | 0 | 0 | 0 | -0,75 | 0 | 1 | 0 | 0 | 0 |
| Σ filles | -1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| Σ garçons | 0 | -1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| Σ foncés | 0 | 0 | 0 | -1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 50 |
résolution avec numpy avec un script Python.
#!/usr/bin/env python3
import numpy as np
M = np.array(
(
[1, -1, 0, 0, 0, 0, 0, 0],
[0.4, 0.4, 0, -1, 0, 0, 0, 0],
[0.6, 0.6, -1, 0, 0, 0, 0, 0],
[0, 0, 0, -0.75, 0, 1, 0, 0],
[-1, 0, 0, 0, 1, 1, 0, 0],
[0, -1, 0, 0, 0, 0, 1, 1],
[0, 0, 0, -1, 0, 1, 0, 1],
[1, 1, 0, 0, 0, 0, 0, 0],
)
)
M_inv = np.linalg.inv(M)
V = np.array((0, 0, 0, 0, 0, 0, 0, 100))
R = np.matmul(M_inv, V)
# print(R)
print("réponse:", R[6])
réponse: 40%
Mercredi 3 Février
- aire triangle = c × a / 2
-
aire trapèze = c × (b + a / 2)
- rapport 4:1 →
- 4 × a / 2 = (b + a / 2)
- 2 a = b + a / 2
- 3/2 a = b ou a = 2/3 b
réponse: b/a = 3/2
Jeudi 4 Février
Calcul avec script Python.
#!/usr/bin/env python3
CONF = (
"x1 + x10 + 13 + 2",
"x1 + x2 + x3 + 2",
"x8 + x9 + x10 + 13",
"x1 + x4 + x6 + 13",
"x5 + x7 + x10 + 2",
"x6 + x8 + 8 + 15",
"x7 + x9 + 8 + 1",
"x3 + x5 + 10 + 1",
# "x2 + x4 + 10 + 15",
)
X = [3, 4, 5, 6, 7, 9, 11, 12, 14, 16]
import numpy as np
import re
M = np.zeros((10, 10))
V = np.zeros((10))
for i, e in enumerate(CONF):
for x in re.findall(r"x(\d+)", e):
M[i, int(x) - 1] = 1
v = 34
for x in re.findall(r" (\d+)", e):
v -= int(x)
V[i] = v
M[9, 0] = 1 # pour fixer x1
M[8, 1] = 1 # pour fixer x2
for x1 in X:
V[9] = x1
for x2 in X:
V[8] = x2
if np.linalg.det(M) == 0:
continue
M_inv = np.linalg.inv(M)
R = np.matmul(M_inv, V)
if set(R) == set(X):
print(R)
réponse: (cf. ci-dessous)
[10]
[14] [ 6] [12] [ 2]
[ 3] [11]
[15] [ 1]
[ 4] [16]
[13] [ 7] [ 9] [ 5]
[ 8]
Vendredi 5 Février
| proposition | interprétation | équation |
|---|---|---|
| Pierre a trois plus de sœurs que de frères | 3 frères = sœurs | 3 (garçons - 1) = filles |
| Pauline a deux fois plus de sœurs que de frères | 2 frères = sœurs | 2 garçons = filles - 1 |
- 2 garçons + 1 = 3 ( garçons - 1) ⇒ garçons = 4
- filles = 1 + 2 garçons ⇒ filles = 9
réponse: 4 garçons, 9 filles
Lundi 8 Février
Cf. programme en Python.
#!/usr/bin/env python3
# il faut les nombres premiers jusqu'à environ 2010^(1/3), soit environ 13. au-delà c'est trop grand (11*13*17 = 2431)
primes = [2, 3, 5, 7, 11, 13]
# calcule le produit de 3 premiers consécutifs
prod3 = []
for a, b, c in zip(primes, primes[1:], primes[2:]):
if a * b * c > 2010:
break
prod3.append(a * b * c)
year = 2009
while year > 0:
for i in prod3:
if year % i == 0:
print("réponse:", year)
break
else:
year -= 1
continue
break
réponse: 2002
Mardi 9 Février
demi-cercle + 2 carrés
- l’angle Θ centre/sommet est 45° (figure symétrique), donc a = √2 / 2
- aire des 2 petits carrés: (√2 / 2)² × 2 = 1
demi-cercle + 1 carré
- il faut que sin Θ = 2 cos Θ
- aire 1 carré: sin Θ × 2 cos Θ = sin² Θ
- or sin² Θ = 1 - cos² Θ = 4 cos² Θ. donc on a cos² Θ = 1 / 5
- aire grand carré: 1 - 1 / 5 = 4 / 5
réponse: 4 / 5
Mercredi 10 Février
+---+---o +---+---+
| I | K | | U | P |
+---+---+ +---o---+
| M | | K |
+---+ +---+
Les faces U et P sont à côté de K (donc derrière et à droite sur le dessin 3D de IKM). Le sens de rotation horaire U→P→K doit être respecté, la disposition est donc la suivante (le o désigne le même sommet du cube):
+---+
| U |
+---+---o---+---+
| I | K | P | |
+---+---+---+---+
| M |
+---+
réponse: M
Jeudi 11 Février
(a + d) + (b + d) + (c + d) = 7 + 10 + 12 = 29 = (a + b + c) + 3 × d
max(d) = 6 car x + d = 7 et x ≥ 1
donc max(a + b + c) = 29 - 3 × 6 = 11
réponse: 11
script Python de recherche de toutes les valeurs
#!/usr/bin/env python3
from itertools import product
# x+d = 12 ⇒1 ≤ a,b,c,d ≤ 11
for a, b, c, d in product(range(1, 12), repeat=4):
s = (a + d, b + d, c + d)
if s == (7, 10, 12):
# uniquement les solutions a < b < c
print(a, b, c, d, "Σ=", a + b + c)
Vendredi 12 Février
Voir factordb, ou wolframalpha.
Ou avec SageMath: factor(101010101010101010101)
Ou encore SymPy: sympy.factorint(101010101010101010101)
etc.
Mais ce n’est certainement la méthode attendue 😇
Il y a onze chiffres 1 aux positions impaires, et que des 0 aux positions paires. Le critère de divisibilité par 11 est rempli.
réponse: 11
Lundi 15 Février
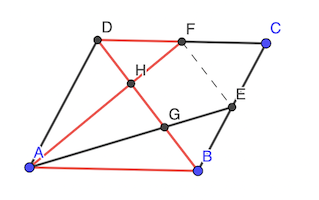
Appliquons le théorème de Thalès:
- DF / AB = HD / HB = HF / HA
- EB / DA = GE / GA = GB / GD
On a:
- DF / AB = 1 / 2 car F est le milieu de [DG] et DG=AB
- HD = 1 cm par énoncé
- idem EB / DA et GB
On en déduit que HB = GD = 2 cm
Or HB = HG + GB donc HG = 1 cm
réponse: 1 cm
Mardi 16 Février
- en dessous du A, on peut mettre B, C, D ⇒ 3 possibilités
- en dessous de la lettre en dessous du A, on peut mettre A ou les 2 autres lettres ⇒ 3 possibilités
- en dessous des 2 autres, on n’a plus le choix puisqu’il reste 1 des 2 autres avec le A, ou les 2 autres
Confirmation avec script Python.
#!/usr/bin/env python3
from itertools import permutations
n = 0
for a, b, c, d in permutations("ABCD"):
if a == "A" or b == "B" or c == "C" or d == "D":
continue
print(a, b, c, d)
n += 1
print("réponse:", n)
réponse: 3 × 3 = 9
Mercredi 17 Février
273 = a + ar + ar² = a (1 + r + r²)
273 = 3 × 7 × 13
1 + r + r² = r (r² - 1) / (r - 1)
- 1 + 1 + 1 = 3 ok
- 1 + 2 + 4 = 7 ok
- 1 + 3 + 9 = 13 ok
- 1 + 4 + 16 = 21 ok
- 1 + 5 + 25 = 31 ko
- 1 + 6 + 36 = 43 ko
- 1 + 7 + 49 = 57 ko
- 1 + 8 + 64 = 73 ko
- 1 + 9 + 81 = 91 ok
- 1 + 16 + 256 = 273 ok
Donc, les possibilités de couple (a, r) sont:
- (91, 1)
- (39, 2)
- (21, 3)
- (13, 4)
- (3, 9)
- (1, 16)
réponse: 6
Jeudi 18 Février
Il fait (2 + 2) km en (12 + 4) min, soit 4 km en 16 min.
V = 1 / 4 km⋅min⁻¹ = 60 / 4 km⋅h⁻¹
réponse: 15 km⋅h⁻¹
Vendredi 19 Février
À dessiner sur une feuille quadrillée…
réponse: 6 cm²
Lundi 22 Février
En une ligne de Python:
python3 -c "print(sum(1 for n in range(1000) if 7==sum(map(int,str(n)))))"
Pour dénombrer à la main, il faut considérer ces choix:
- 7 0 0
- 3 4 0
- 2 5 0
- 1 6 0
- 1 2 3
- 1 3 3
Avec 3! = 6 possibilités chaque, soit 36 en tout.
réponse: 36
Mardi 23 Février
Il faut que le nombre se termine par un chiffre pair, donc tous les chiffres doivent être pairs.
De plus les deux derniers chiffres doivent constituer un nombre divisible par 4: pas 02, 10, 06. Il ne reste que le 4 et le 8, soit 2^3=8 solutions.
réponse: 8
Mercredi 24 Février
Si l’essence est vendue 100:
- 65 taxes
- 35 production
Si l’essence coûte 35:
- 35 * 0.76 = 26.6 production
- 35 * 0.24 = 8.4 pétrole
Le pétrole passe à 8.4 + 10% = 9.24
Le prix de l’essence devient 65 + 26.6 + 9.24 = 100.84
Soit une augmenation de 0.84%
réponse: 0.84%
Jeudi 25 Février
L’aire des carrés avec intersection est 117 + 2 + 5 + 8 = 132 cm². L’aire des trois carrés est donc 132 + 2 + 5 + 8 = 147 cm².
Le côté est √(147/3) = √49 = 7 cm
réponse: 7 cm
Vendredi 26 Février
27000 = 27 × 8 × 125 = 2³ × 3³ × 5³
a × ar × ar² = a³ r³
On peut choisir (1, 30) (2, 15) (3, 10) (5, 6) et vice-versa pour (a, r).
réponse: 8