Calendrier Mathématique Juillet 2021
Jeudi 1 Juillet
Cf. programme Python.
#!/usr/bin/env python3
for i in range(11, 100):
a, b = divmod(i, 10)
if (a + b) * 5 == i - (a + b * 10):
print(i)
réponse: 72
Vendredi 2 Juillet
Cf. programme Python.
#!/usr/bin/env python3
n = 0
for i in range(11, 100):
a, b = divmod(i, 10)
if a != 0 and b != 0:
if i % a == 0 and i % b == 0:
print(i)
n += 1
print("réponse:", n)
réponse: 14
Lundi 5 Juillet
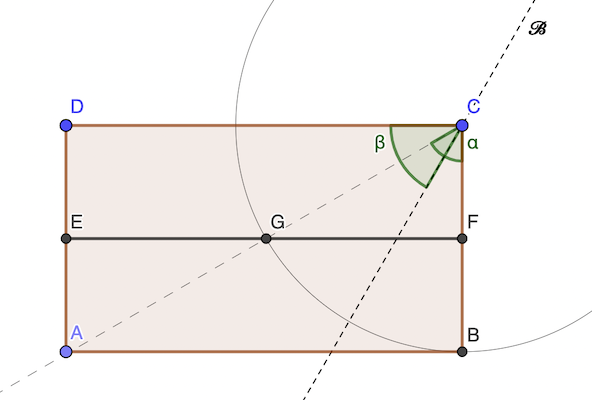
On doit avoir: CG = CB puisque la droite 𝓑 est la bissectrice de GCB.
Donc G est sur le cercle de centre E et de rayon CB.
cos 𝜶 = 1 / 2 𝜶 = 60°
𝜷 = 90° - 𝜶 / 2 = 60°
réponse: 60°
Mardi 6 Juillet
Ecrivons le fait que la moyenne après 𝑥 examens avec une note de 10 doit être supérieure ou égale à 9:
(8.3 × 5 + 10 × 𝑥) / (5 + 𝑥) ≥ 9 et 𝑥 entier
41.5 + 10 𝑥 - 9 𝑥 - 45 ≥ 0
𝑥 ≥ 3.5
Il faut au moins quatre 10 pour remonter la moyenne à plus que 9.
réponse: 4
Mercredi 7 Juillet
si a,c pairs: on a la somme de quatre nombres impairs, résultat pair
si a,c impairs: somme de quatre pairs, résultat pair
si a,b impair/pair: somme de 2 pairs et 2 impairs, résultat pair
réponse: pair
Jeudi 8 Juillet
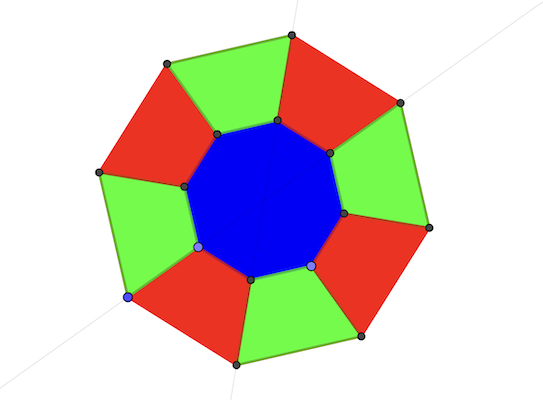
Il y a 6 dispositions de couleur (3 pour le centre, puis 2 pour alterner les secteurs).
réponse: 6
Vendredi 9 Juillet
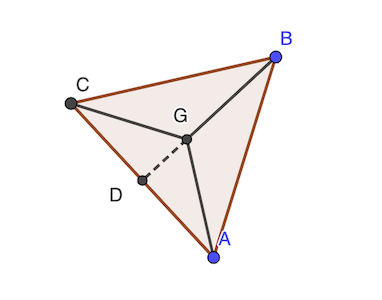
Les triangles isocèles sont équivalents à GAB GBC GCA, G = centre du triangle ABC (orthocentre, barycentre, cercles inscrit et circonscrit).
Pythagore permet de calculer AG:
AG² = (½ AG)² + (½)²
4 AG² - 3 AG² = 1
AG = 1 / √3
réponse: 1 / √3 cm
Lundi 12 Juillet
Soit Vr la vitesse de la rameuse et Vc celle du courant. Soit la d la distance parcourue dans un sens.
d = (Vr - Vc) * 3h = (Vr + Vc) × 2h
D’où: 3 Vr - 3 Vc = 2 Vr + 2 Vc ⇒ Vr = 5 Vc
d = Vr (1 + 1 / 5) * 2h ⇒ Vr = d / 2 × 5 / 6 = 5 / 12 d ⇒ d / Vr = 12 / 5
Pour parcourir 2 d, la rameuse va prendre: 2 d / Vr = 2 × 12 / 5 = 24 / 5 h
En minutes: 60 * 24 / 5 = 288, soit 240 + 48 ou encore 4h48
réponse: 4h48
Mardi 13 Juillet
11^x se termine toujours par 1 et 5^y toujours par 5. Donc la différence minimale est au moins 4.
Or celle-ci est atteinte pour x=2 et y=3. On ne pourra jamais faire moins.
réponse: 4
Mercredi 14 Juillet
20 + 40 + 45 = 105
105 billes en tout, réparties équitablement sur 3 sacs: 105 / 3 = 35 billes par sac.
réponse: 35
Jeudi 15 Juillet
angle ∠FDE = 90° car ∠FDC = 60° et ∠CDE = 90 - ∠EDA = 90° - 60° = 30°
donc DE² = 8 × 2 = 16 et DE = 4 cm, qui est aussi AB
réponse: 4 cm
Vendredi 16 Juillet
a != c sinon le trajet aurait duré 0h (l’énoncé ne le précise pas mais le sous-entend).
Donc le nombre d’heures est impair sinon (5 × 2k + c) mod 10 = c et on aurait a = c.
On obtient l’inégalité suivante: (c + 5) mod 10 = a ≥ 1
Si a=1 c=6 et b=0 et pas de solution si a ≥ 2, c vaudrait au moins 7 ce qui contredit a + b + c ≤ 7
Vérification: 601 - 106 = 496 = 55 × 9
réponse: 106
Lundi 19 Juillet
(10a + u)² = 100a² + 20au + u²
Il faudrait donc (a,u) tel que 2au + E(u² / 10) = u² (mod 10) avec u impair i.e. chiffre des dizaines = unité.
Le chiffre des dizaines de u² est toujours pair (0, 2, 4, 8). Ce qui revient à écrire: 2au + pair = u²
Ainsi u² serait pair, donc u également, ce qui est en contradiction avec l’hypothèse.
Donc u ne peut pas être impair. En revanche, il peut être pair. Exemple: 100
réponse: non
Mardi 20 Juillet
frère Léa => Léa n’est pas mathématicienne.
Océane plus jeune que ingénieure => comme mathématicienne plus âgée, Océane est la plus jeune et physicienne.
Léa est donc ingénieure.
La seule possibilité restante est Marie mathématicienne.
réponse: mathématicienne
Mercredi 21 Juillet
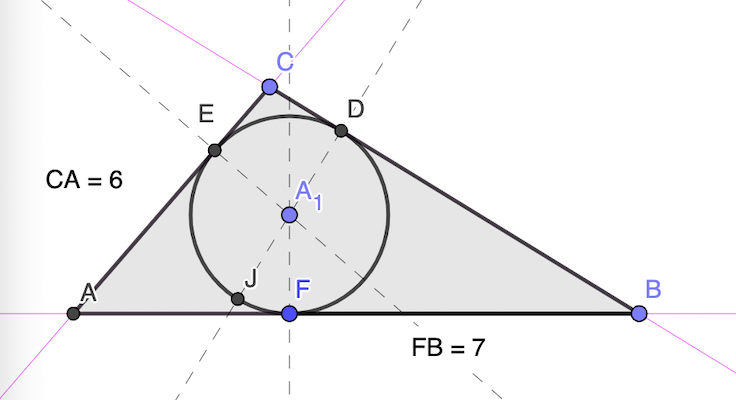
On a BF = DF, AE = AF, EC = DC (car DFB etc. sont isocèles)
p = BF + BD + AF + AE + CE + CD
= 7 + 7 + (AF + CD) + (AE + CE)
= 7 + 7 + 6 + 6
= 26
réponse: 26 cm
Jeudi 22 Juillet
On doit avoir 62424 / (30 + u) = entier. Décomposons 62424 en produit de facteurs premiers :
62424 = 2 × 2 × 2 × 3 × 3 × 3 × 17 × 17
On a deux candidats entre 30 et 39: 36 et 34
1734 1836
× 36 × 34
------ ------
10404 7344
5202. 5508.
------ ------
62424 62424
C’est la deuxième multiplication qui correspond aux étoiles.
réponse: 1836 × 34
Vendredi 23 Juillet
On doit avoir n × 31 + r = 500. r est donc le reste de la division entière de 500 par 31, soit 4.
réponse: 4
Lundi 26 Juillet
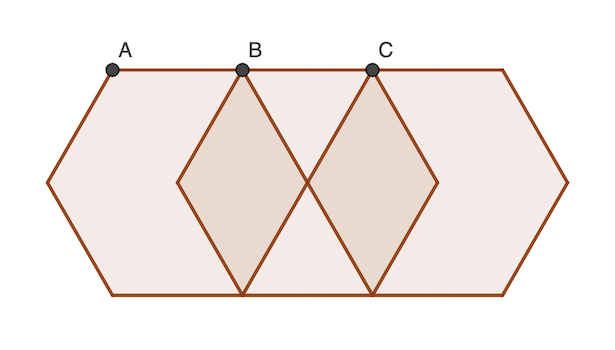
On considère les hexagones ayant un côté supérieur sur la ligne du haut, le côté inférieur sur la ligne de bas, et les autres côtés sur les lignes brisées reliant le haut du bas.
Hexagones ayant le sommet haut gauche sur le point:
- A: 5
- B: 2 × 3
- C: 2 × 1
réponse: 12 hexagones
Mardi 27 Juillet
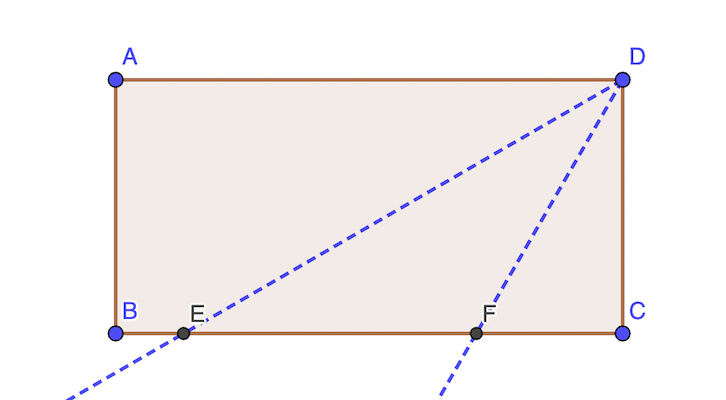
AD / EA = tan 30° AD / FA = tan 60°
EA - FA = AD / tan 30° - AD / tan 60° = AD × (√3 - 1 / 3) = AD × 2 V3 / 3
aire DEF = AD × EF / 2 = AD² × √3 / 3
aire ABCD = DC × BC = 2 × BC × BC = 2 × AD²
rapport aire DEF / aire ABCD : √3 / 6
réponse: √3 / 6
Mercredi 28 Juillet
C’est 2021 répété 2020 / 4 = 505 fois.
La somme des chiffres est donc 5 × 505 = 2525
Il faut enlever 504, soit au mieux 252 chiffres 2 (puisqu’il n’y a que des 0, 1, 2).
réponse: 252
Jeudi 29 Juillet
- x₀ = 1
- xₙ₊₁ = xₙ × 2 + 1
On obtient successivement les nombres 1, 3, 7, 15, etc.
Montron que f(n) = 2ⁿ⁺¹ - 1.
f(n + 1) = 2 × f(n) + 1 = 2 × (2ⁿ⁺¹ - 1) + 1 = 2ⁿ⁺² - 1.
Donc f(12) = 2¹³ - 1 = 8192 - 1 = 8191
réponse: 8191
Vendredi 30 Juillet
On place les moutons: ▢ M ▢ M ▢ M ▢ M ▢ M ▢
Il y a 6 places libres ▢ pour placer les 4 chiens.
- Nombre de permutations des moutons: 5! = 120
- Nombre de permutations des chiens: 4! = 24
- Nombre de placements des chiens dans ▢: C(6, 4) = (6! / (4! × (6 - 4!)) = 15
- Donc: N = 120 × 24 × 15 = 43200
Vérification en Python:
import itertools
sum(1 for i in itertools.permutations("CCCCMMMMM") if "".join(i).find("CC") == -1)
réponse: 43200