Calendrier Mathématique Mars 2021

Solutions 2021 - Homepage

Lundi 1 Mars

Voir script Python.

#!/usr/bin/env python3

import itertools

n = 0
for fruits in itertools.product("AP", repeat=6):
    for i in range(6 - 2):
        if fruits[i] == "A" and fruits[i + 1] == "P" and fruits[i + 2] == "A":
            break
    else:
        n += 1
        # print(" ".join(fruits))

print("réponse:", n)

réponse: 37

Mardi 2 Mars

(a+b)³ = a³ + 3ab² + 3a²b + b³

(10²⁰²¹)³ = 100…000 ⇒ Σ chiffres = 1
3 × 10²⁰²¹×1² = 3 × 100…000 ⇒ Σ chiffres = 3
3 × (10²⁰²¹)² × 1 = 3 × 100…000 ⇒ Σ chiffres = 3
1³ = 1 ⇒ Σ chiffres = 1

réponse: 8

Mercredi 3 Mars

Il faut que x¹⁰ - 4 soit divisible par x². Donc x² doit diviser 4.

Donc x = ±1 ou x = ±2

• Si x = ±1, 1 + k + 4 = 0 ⇒ k = -5
• Si x = ±2, 1024 + 4k + 4 = 0 ⇒ k = -1028 / 4 = - 257

réponse: -5 et -257

Jeudi 4 Mars

• volume sphère: 4/3 πR³
• surface sphère: 4πR²

V₂ / V₁ = 2 = (4/3 πR₂₁³) / (4/3 πR₁³) = (R₂ / R₁)³ = 2

S₂ / S₁ = (4πR₂²) / (4πR₁²) = (R₁ / R₂)² = 2⁽²/³⁾ = ∛4

réponse: ∛4

Vendredi 5 Mars

Toutes les faces du dé à 4 faces peut se combiner avec une face du dé à 8 faces pour faire 11: 1+10, 3+8, 5+6, 7+4

Donc seule la face du dé à 8 faces compte.

réponse: 1/8

Lundi 8 Mars

Il reste 10 l après la première couche. 3/4 * 10 = 7.5 l. On a utilisé 10 + 7.5 = 17.5 l de peinture, il reste donc 20 l sur les 20.

réponse: 2.5 l

Mardi 9 Mars

Analyse:

• Wookies = vérité ⇒ ils répondent 1 oui 2 non
• Jawas = mensonge ⇒ ils répondent 2 oui 1 non

Mise en équation:

• le nombre de oui ⇒ 3000 = Jawas × 2 + Wookies (1)
• le nombre d’habitants ⇒ 2021 = Jawas + Wookies (2)

Résolution:

• 2 × (2) - (1) : 2021 × 2 - 3000 = Wookies = 1042

réponse: 1042

Mercredi 10 Mars

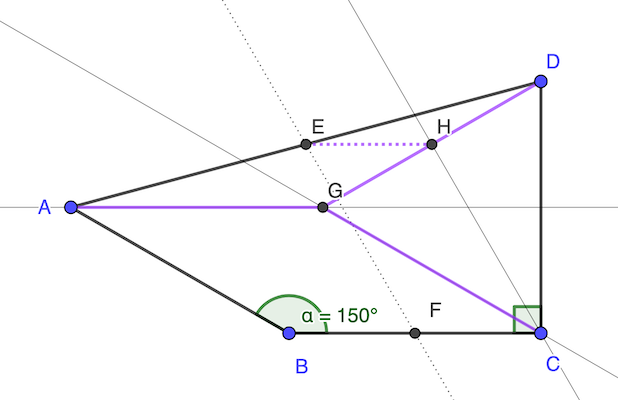
Traçons le parallèlogramme ABCG.

On a CG=AB=DC. Donc le triangle GCD est isocèle en C.

L’angle ∠GCD vaut 90° - ∠BCD = 90° - 30° = 60°. Ainsi, le triangle GCD est équilatéral et GD=AB=CG=DC.

Soit H le milieu de GD. Thalès permet d’affirmer que EH // AG et EH = 1/2 AG puisque E défini comme le milieu de AD.

Ainsi EH et FC sont // et de même longueur, le quadrilatère EHCF est un parallèlogramme.

L’angle ∠GCH vaut 30° (bissectrice), et par conséquence, l’angle ∠BCH est égal à 60°.

réponse: 60°

Jeudi 11 Mars

On a le facteur 2^15: on considère les nombres pairs:

pairs:   2 - 4 - 6 - 8 - 10 - 12 - 14 - 16
nb de 2: 1   2   1   3    1    2    1    4

Deux candidats: 16! ou 17!. Mais 17 est premier et il n’est pas dans la décomposition de n!. C’est donc 16!.

réponse: n = 16

Vendredi 12 Mars

Soit (a,b,c) avec 0 ≤ a < b < c ≤ 99 le tirage des 3 jetons.

Si a= 0, pas de solution car on aurait b=c
Si a= 1, b 2-98 et c doit valoir 3-99
Si a= 2, b 3-97 et c doit valoir 5-99
Si a= 3, b 4-96 et c doit valoir 7-99
…
Si a=48, b 49-50 et c doit valoir 98-99
Si a=49, b 50-50 et c doit valoir 99-99
Si a=50, b≥51 et pas de valeur possible pour c

Nombre de valeurs de b = (98 - 2 + 1) - (a - 1) × 2 pour a ∈ [1, 49]

Σ (97 - i × 2) = 49 × 97 - 48 × 49 × 2 / 2 = 2401
i ∈ [0, 48]

Vérification en Python:

python3 -c 'print(sum(1 for a in range(0, 98) for b in range(a + 1, 99) for c in range(b + 1, 100) if a + b == c))'

réponse: 2401

Lundi 15 Mars

Les deux règles sont alignées sur le repère 3.5 cm. La longueur jusqu’à l’extrémité est 6.5 cm. La longueur totale est donc 6.5 × 2 = 13 cm

réponse: 13 cm

Mardi 16 Mars

n = 1 ⇒ 5 n + 7 = 12 divisible par 3, donc n = 1 + 3k conviennent. k de 0 à 33 permet d’avoir n entre 1 et 100.

réponse: 34

Mercredi 17 Mars

Carrés à 2 chiffres: 16 25 36 47 63 81

Critère de divisibilité par 11: Σ (chiffres de rang pair) - Σ (chiffres de rang impair) divisible par 11

Ici, cette différence vaut au moins 2: on peut donc toujours trouver un et un seul chiffre qui convient. Pour en trouver 2, il faudrait ajouter ou soustraire 11 au chiffre ajouté, ce n’est pas possible. Les solutions sont: 616 825 836 847 363 781

En tirant un chiffre en 1 et 9, on a une chance sur 9 de tomber sur le bon.

réponse: 1 / 9

Jeudi 18 Mars

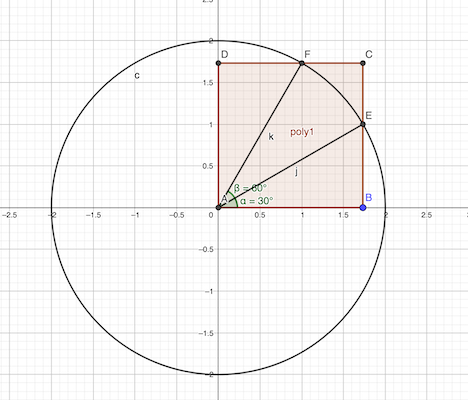
Calcul partie courbe

• AB = √12 / 2 = √3
• AE = 2
• cos 𝜶 = √12 / 2 / 2 = √3 / 2 donc 𝜶 = 30°
• sin 𝜷 = √3 / 2 donc 𝜷 = 60°

Chaque quart de la figure est constitué de 2 arcs de 30° du cercle de rayon 2 cm.

La partie courbe est donc: (8 × 30 / 360) × 2 × 2 π = 8 / 3 π

Calcul partie droite

CE = CB - EB = √12 / 2 - 2 × sin 30° = √3 - 2 / 2

La partie droite est donc: 4 × 2 × (√3 - 1) = 8 √3 - 8

réponse: 8 / 3 π + 8 √3 - 8 cm

Vendredi 19 Mars

xy = 4(y² + x) ⇒ (y - 4) x = 4 y² Donc y - 4 divise 4 y²

Or 4 y² = 4 (y - 4) (y + 4) + 64 Donc y - 4 divise aussi 4 (y - 4) (y + 4) + 64 et par conséquent doit aussi diviser 64.

Les diviseurs entiers signés de 64 sont: ±1 ±2 ±4 ±8 ±16 ±32 ±64

Ce qui donne une valeur pour y. Celle de x s’en déduit et est unique. Il y a donc 14 couples possibles.

Script Python de vérification (mais pas de résolution).

#!/usr/bin/env python3

for sign in [-1, 1]:
    for exp in range(0, 7):
        y = sign * 2 ** exp + 4
        x = 4 * y ** 2 // (y - 4)
        print(f"x={x:4}, y={y:4} {x * y == 4 * (y ** 2 + x)}")

réponse: 14

Lundi 22 Mars

8000 = 20³
27000 = 30³
Donc le nombre est strictement compris entre 20 et 30.

Or, pour se terminer par 7, il faut que le nombre se termine par 3 (3³ = 27). En effet, le chiffre des unités d’un cube est celui du cube du chiffre de l’unité:

(10a + u)³ = 1000a³ + 3 × 100a² × u + 3 × 10a × u² + u³ = 10 × […] + u³

C’est donc 23 et 23³ = 12167.

réponse: 23

Mardi 23 Mars

La probabilité de n’avoir que des mauvaises réponses pour une ligne est 1 - 1 / n.
La probabité de n’avoir que des mauvaises réponses est ∏ (1 - 1 / n).
La probabilité d’avoir au moins une bonne réponse est 1 - ∏ (1 - 1 / n).

p = 1 - (1 - 1 / 2) × (1 - 1 / 3) × … × (1 - 1 / 12)
= 1 - (1 / 2) × (2 / 3) × … × (11 / 12)
= 1 - 11! / 12!
= 1 - 1 / 12
= 11 / 12

réponse: 11 / 12

Mercredi 24 Mars

Soit v la longueur de la grande diagonale.

Formule de Héron:
  S = √(p(p - a)(p - b)(p - c))

avec p = (a + b + c) / 2

p = (v + 1 + 2) / 2
p - a = (v + 3) / 2 - v = (3 - v) / 2
p - b = (v + 3) / 2 - 1 = (v + 1) / 2
p - c = (v + 3) / 2 - 2 = (v - 1) / 2

S² = 1 = ¹/₁₆ × (3² - v²) * (v² - 1)

On pose V = v²

(9 - V) (V - 1) = 16

9 × V - 9 - V² + V = 16 V² - 10 * V + 25 = 0 (V - 5)² = 0

Donc v = √5

réponse: √5

Jeudi 25 Mars

Multiples de 6 de 1 à 400: 6, 12, … 396 ⇒ 66 valeurs

Multiples de 1 à 40: 6, 12, 18, 24, 30, 36 ⇒ 6 valeurs

Les habitants vont perdre: 66 - 6 × 10 = 6

réponse: 6

Vendredi 26 Mars

8 triangles isocèles:

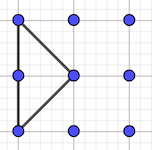
8 triangles quelconques:

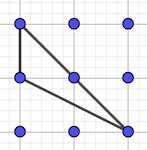
16 triangles rectangles:

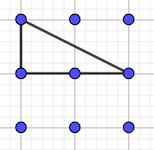
réponse: 32

Lundi 29 Mars

C’est la pièce qui a le plus de côtés puis de côtés obliques. Ce genre de côté sera plus qu’un côté droit.

réponse: E

Mardi 30 Mars

Soit a ≤ b ≤ c ≤ d ≤ e les cinq nombres positifs.

Pour qu’un nombre divise toujours un autre il faut avoir:

• b = k⋅a
• c = k’⋅b = k’⋅k⋅a
• etc.

n = a + b + c + d + e = a + k⋅a + k’⋅k⋅a + … = a × (1 + k + k’⋅k + …)

Donc a divise toujours n. Pour que n soit premier il est nécessaire que a = 1.

réponse: a = 1

Mercredi 31 Mars

Le triangle n’a pas de diagonale.

Un polygone régulier à n côtés a n-3 diagonales par sommet.

Soit en tout, en ne comptant pas 2 fois les mêmes diagonales : n (n - 3) / 2

n (n - 3) / 2 = n ⇒ n - 3 = 2 ⇒ n = 5

réponse: le pentagone