Calendrier Mathématique Avril 2022

Solutions 2022 - Homepage

Vendredi 1 Avril

Formule de Héron aire triangle avec ses côtés:

• p = (a + b + c) / 2
• A = √(p × (p - a) × (p - b) × (p - c))

Soit x la longueur du côté inconnue, x > 0.

On a donc:

• 16 * A² = 2p (2p - 2a) (2p - 2b) (2p - 2c)
• a = 13, b = 10, c = x
• p = (x + 23) / 2
• 16 * 60² = (x + 23) (x + 23 - 26) (x + 23 - 20) (x + 23 - 2x)
• 57600 = (x + 23) (x - 3) (x + 3) (-x + 23)
• 57600 = (23² - x²) (x² - 3²)

On obtient donc l’équation du second degré en X = x² :

X² - 538 X + 62361 = 0

X = (+538 ± √(538² - 4*62361)) / 2 = (538 ± 200) / 2 = 169 ou 369

Donc x = √X = 13 ou 3 √41

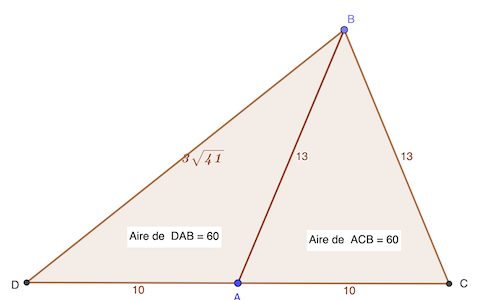
Nota

Complément de solution par rapport à celle du livret: le triangle rectangle constitué avec la hauteur peut se construire à l’ « extérieur » de la base, ce qui donne un autre résultat (3√41 en l’occurrence).

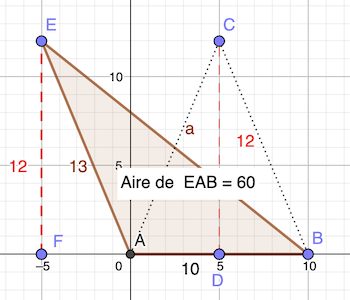
réponse: 13 cm ou 3 √41 cm ⚠️

Lundi 4 Avril

Après avoir réécrit l’expression sous forme de produit de fractions, on simplifie deux à deux les termes identiques:

\[\begin{aligned} E&=\prod_{k=8}^{70}{\left(1-\frac{1}{k^2}\right)} \\ &=\prod_{k=8}^{70}{\frac{k^2-1}{k^2}} \\ &=\prod_{k=8}^{70}{\frac{(k-1)(k+1)}{k^2}} \\ &=\frac{7\times{\cancel{9}}}{8\times{\cancel{8}}}\times\frac{ {\cancel{8}}\times{\cancel{1}0}}{ {\cancel{9}}\times{\cancel{9}}}\times\frac{ {\cancel{9}}\times{\cancel{11}}}{ {\cancel{10}}\times{\cancel{10}}}\times\cdots\times\frac{ {\cancel{69}}\times{71}}{ {\cancel{70}}\times{70}} \\ &=\frac{7}{8}\times\frac{71}{70} \\ &=\frac{71}{80} \end{aligned}\]

réponse: 71/80

Mardi 5 Avril

Un nombre se termine par 0 si et seulement s’il est multiple de 2 et de 5, respectivement par n 0, 2ⁿ et 5ⁿ.

Donc si a = 2¹⁰ × 100000 et b = 5¹⁰ × 100000, alors a × b = 10²⁰.

réponse: oui

Mercredi 6 Avril

L’aire recherchée vaut h × 2 / 2 + h × 2 / 2 = 2 h (avec h = IJ = BJ)

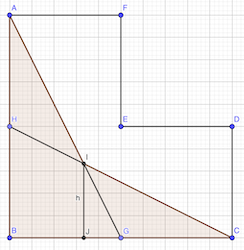
Le point I est à l’intersection des droites d’équation:

• y = -2x + 2 (droite AG)
• y = -x/2 + 1 (droite CH)

-2x + 2 = x/2 + 1 ⇒ -4x + 4 = x + 2 ⇒ 2 = 3 x ⇒ x = 2/3

Les coordonnées du point I sont (2/3; 2/3). D’où l’aire = 2 × 2/3 = 4/3 cm²

réponse: 4/3 cm²

Jeudi 7 Avril

Dans un carré 4x4, on peut dessiner au maximum 5 rectangles 3x1 ou 1x3. Il faut donc supprimer au minimum 5 cases.

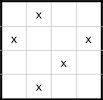
réponse: 5

Vendredi 8 Avril

Déterminons la valeur de $xy+yz+zx$:

\[\frac 1 x + \frac 1 y + \frac 1 z = \frac {xz+yz + xy} {xyz} = \frac 3 4\]

D’où: $xy+yz+zx=\frac 3 4\times 72=54$

On peut maintenant calculer $x^2 + y^2 + z^2$:

\[x^2 + y^2 + z^2 = (x+y+z)^2 - \left( 2xy + 2yz + 2zx\right) ={13}^2-\left(2\times{54}\right)=169-108=61\]

réponse: 61

Lundi 11 Avril

Dans un quadrillage carré de taille impaire, il y a un nombre impair de carrés formant les diagonales (5 pour une grille 3×3).

Le quadrillage est donc de taille paire, et le nombre de carrés formant une diagonale est la taille du côté. Les diagonales n’ont pas de carrés en commun.

Donc la mosaïque a pour côté 1616/2 = 808. Il y a en tout 652864 carrés, dont 1616 bleus et donc 651248 rouges.

réponse: 651248

Mardi 12 Avril

Le théorème des bissectrices d’un triangle permet d’écrire:

\[\frac {AB} {AC} = \frac {DB} {DC}\]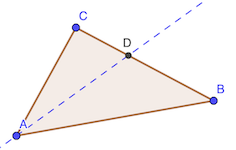

On peut calculer la longueur $AB+BD$: \(\frac {AB} {AC} = \frac {DB} {DC}= \frac {AB+DB} {AC+DC} =\frac{AB+DB}{12}=2\)

car

\[CD=\frac 1 3 BC = \frac 1 3 \left( BD+CD \right) \implies BD=2 CD\]

Le périmètre du triangle est donc:

\[AB+BC+CA= (AB+BD)+(DC+CA)=2\times 12+12=36\]

réponse: 36 cm

Mercredi 13 Avril

Si n a 6 diviseurs, alors sa décomposition en facteurs premiers peut être:

• p²⋅q où p et q sont premiers → 1, p, p², p⋅q, q, p²⋅q
• p⁵ où p est premier → 1, p, p², p³, p⁴, p⁵

Dans le premier cas, n² = p⁴⋅q² → 5×3 = 15 diviseurs.

Dans le deuxième cas, n⁵ = p¹¹ → 11 diviseurs.

réponse: 11 ou 15

Jeudi 14 Avril

x⁴y⁴ est toujours positif, donc le facteur restant yz doit être strictement positif.

réponse: yz > 0

Vendredi 15 Avril

Soit n un nombre entier positif qui est égal au produit de n nombres entiers dont la somme est 0. Est-ce que n doit être pair ou impair ?

Cela fonctionne avec n pair, avec au moins la solution pour n=4 : $\prod = (-1) \cdot 1 \cdot (-2) \cdot 2 = 4\text{, }\sum=1-1+2-2=0$.

Mais aussi pour n=16: $\prod = {(-1)}^6 \cdot {(-2)}^2 \cdot 1^6 \cdot 2^2=16\text{, }\sum=0$ N+P=0.

Supposons à présent n impair.

Soit N l’ensemble des nombres négatifs et P l’ensemble des nombres positifs. Ces deux ensembles sont exclusivement de nombres impairs, pour que leur produit soit égal à n, impair. De plus, N + P = 0.

Pour que le produit soit positif il faut card(N) pair. Donc N est également pair, puisque impair+impair=pair.

Or card(P) = n - card(N) est impair (impair-pair=impair). Mais la somme d’un nombre impair de nombres impairs est impaire. P et N ont la même parité (N+P=0), et P ne peut pas être à la fois pair et impair.

D’où la condradition qui entraine l’impossibilité de n impair.

réponse: n doit être pair

Lundi 18 Avril

Pour M / N soit maximal, il faut M le plus grand possible et N le plus petit possible. M vaut au maximum 999, N au minimum 100. Le rapport vaut au maximum 9.99, soit 9 puisque il doit être entier. Donc M = 999 et N = 111.

réponse: 9

Mardi 19 Avril

a est un diviseur de $100 = 2^2 \times 5^2$.

c est un diviseur de $140 = 2^2 \times 5 \times 7$.

Ainsi, b est un diviseur de $2^2 \times 5$, soit 6 valeurs possibles.

Programe en Python:

#!/usr/bin/env python3

for a in range(1, 141):
    for b in range(1, 141):
        for c in range(1, 141):
            if a * b == 100 and b * c == 140:
                print(a, b, c)

réponse: 6

Mercredi 20 Avril

Soit H l’aire de l’hexagone dessiné par l’intersection des deux triangles.

L’aire du premier triangle est:

• A1 = H + 2 + 2 + 4
• A2 = H + x + 1 + 2

Comme les triangles sont superposables, on a A1=A2.

D’où: x = H + 2 + 4 - H - 1 - 2 = 5

réponse: 5

Jeudi 21 Avril

Pour les nombres à n chiffres, il y a 9ⁿ possibilités. Soit 9 + 9 × 9 + 9 × 9 × 9 = 819 jusqu’à 999.

Entre 1100 et 1200, il y a 9×9 supplémentaires, soit 900 en tout.

Idem entre 1200 et 1300, il y a 9×9 supplémentaires, soit 981 en tout.

Chaque dizaine apporte ensuite 9 nombres supplémentaires: jusqu’à 1330 il y aura 999 nombres. Le suivant et millième est donc 1331.

Nota: 1331 est l’écriture de 1000 en base 9.

Exemples de conversion en Python et en Rust:

import numpy
print(int("1331", 9))
print(numpy.base_repr(1000, 9))

extern crate num_bigint;
use num_bigint::BigUint;

fn main() {
    println!("{}", u32::from_str_radix("1331", 9).unwrap());
    println!("{:?}", BigUint::from(1000u32).to_radix_be(9));
}

Vérification par comptage en Python:

#!/usr/bin/env python3

n = 0
i = 0
while True:
    if "0" not in str(i):
        n += 1
        if n == 1000:
            print(i)
            break
            break
    i += 1

réponse: 1331

Vendredi 22 Avril

Soient $a$ et $b$ les chiffres des dizaines et des unités. Ils doivent vérifier l’équation: $a\times b+2a+2b=10a+b$ qui se simplifie en: $a\times(8-b)=b$.

• $a=1\implies 8-b=b\implies b=4$
• $a=2\implies 16=3b\implies \text{pas de solution pour }b$
• $a=3\implies 24=4b\implies b=6$
• $a=4,5,6\implies \text{pas de solution pour }b$
• $a=7\implies 56=8b\implies b=7$
• $a=8,9\implies \text{pas de solution pour }b$

Programme en Rust:

fn main() {
    println!(
        "{:?}",
        (1..=100)
            .filter(|n| *n == (n / 10) * (n % 10) + 2 * ((n / 10) + (n % 10)))
            .collect::<Vec<_>>()
    );
}

Et en Python:

print(list(n for n in range(1, 101) if n == (n // 10) * (n % 10) + 2 * ((n // 10) + (n % 10))))

réponse: 14 36 77

Lundi 25 Avril

Il a acheté 27 bonbons, il en a reçu 5 gratuits, donc 27 + 5 = 32.

réponse: 2.70€

Mardi 26 Avril

500 000 007 × 499 999 993 = (500 000 000 - 7) × (500 000 000 + 7) = (5⋅10⁸)² - 7² = 250 000 000 000 000 000 - 49 = 249 999 999 999 999 951

La somme des chiffres vaut 2 + 4 + 5 + 1 + 9 × 14 = 138

sum(int(c) for c in str(500_000_007 * 499_999_993))

réponse: 138

Mercredi 27 Avril

On peut prendre tous les nombres pairs ou tous les nombres impairs.

réponse: 15

Jeudi 28 Avril

Les diagonales d’un rectangle se coupent en leur milieu et sont de même longueur.

Ainsi dans le rectangle ABCE, on a AD=CD : D est donc le milieu de la diagonale CB et donc de AE.

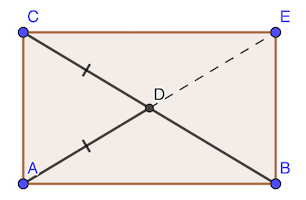
réponse: 10 cm

Vendredi 29 Avril

Il faut que n+4 ou n+2 soit multiple de 7.

n+4 est multiple de 7 pour n=7k+3 : 3, 10, 17, … 94. Soit (94-3)/7+1=14 valeurs.

n+2 est multiple de 7 pour n=7k+5 : 5, 12, 19, … 96. Soit (96-5)/7+1=14 valeurs.

Programme en Rust:

fn main() {
    println!(
        "{:?}",
        (1..=100)
            .filter(|n| (n + 4) * (n + 2) % 7 == 0)
            .collect::<Vec<_>>()
    );

    println!(
        "{}",
        (1..=100).filter(|n| (n + 4) * (n + 2) % 7 == 0).count()
    );
}

réponse: 28