Calendrier Mathématique Juillet 2022

Solutions 2022 - Homepage

Vendredi 1 Juillet

Soit $x=10b+a,y=10c+b,x^2=y^3$. Que vaut $a+b+c$ ?

Si on ramène les nombres à leur décomposition en facteurs premiers, on voit que $x$ doit être un cube et $y$ un carré. Or, les cubes à deux chiffres sont 27 et 64.

On a donc pour choix $b=2, a=7$ ou $b=6, a=4$, et donc $y=\sqrt[3]{ {27}^2}={\left(\sqrt[3]{27}\right)}^2=3^2=9$ ou $y=\sqrt[3]{ {64}^2}=16$.

La première solution ne convient pas car $b$ vaudrait 0 ce qui est contraire à l’énoncé.

La deuxième implique $a=4$ et $b=6$, ce qui est correct. Donc $c=1$.

$a+b+c=4+6+1=11$

réponse: 11

Lundi 4 Juillet

    S E R V I
  ×         4
  ───────────
    I V R E S

On part de I=8 et S=2, puis E=1 pour éviter la retenue, etc.

    2 1 9 7 8
  ×         4
  ───────────
    8 7 9 1 2

réponse: 21978 × 4 = 87912

Mardi 5 Juillet

n² + 6n = n (6 + n)

Pour qu’il n’y ait qu’un diviseur premier, il faut que n et n+6 soient une puissance d’un nombre premier. Et que ce nombre premier divise aussi n+6, donc 6.

n=1 convient car 6+1=7 et 7 est premier.

6 est divisible par 2 et par 3: 2×(2+6)=16=2⁴, 3×(3+6)=27=3³

réponse: 1 2 3

Mercredi 6 Juillet

Il faut résoudre dans 𝐍 ab = 2(a+b).

• ab - 2a - 2b = 0
• a(b - 2) - 2(b - 2) - 4 = 0
• (a - 2)(b - 2) = 4

On en déduit que a-2 et b-2 sont des diviseurs de 4.

Donc a peut valoir 4+2 ou 2+2 ou 1+2, et b respectivement 1+2, 2+2, 4+2.

Ce qui donne soit un carré 4×4 soit un rectangle 6×3. Ou bien soit n=16 soit n=18.

réponse: 16 et 18

Jeudi 7 Juillet

voyage	reste sur rive 1	aller	retour	reste sur la rive 2
1	H1 H2 F3 H3	F1 F2	F1	F2
2	H1 H2 H3	F1 F3	F1	F2 F3
3	H2 H3	F1 H1	F2	F1 H1 F3
4	H3	F2 H2	F3	F1 H1 F2 H2
5		F3 H3		F1 H1 F2 H2 F2 H3

réponse: oui, en 9 trajets

Vendredi 8 Juillet

On a $xy=4(y-x)$.

\[\frac{2y+12(y-x)-2x}{y-x-8(y-x)} =\frac{(12+2)(y-x)}{(1-8)(y-x)} =-\frac{14}7=-2\]

réponse: -2

Lundi 11 Juillet

réponse: 8.50€

Mardi 12 Juillet

L’aire du carré jaune est 25 cm² donc son côté 5 cm et sa diagonale 5√2 cm. Cette dernière est le diamètre du petit cercle, qui est aussi le côté du carré médian. La diagonale du carré médian est dans 5√2×√2 = 10 cm, qui est le diamètre du grand cercle, et le côté du carré ABCD.

réponse: 100 cm²

Mercredi 13 Juillet

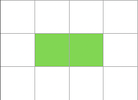
réponse: les deux carrés au milieu

Jeudi 14 Juillet

La condition $15a-13b=1$ peut s’écrire:

\[b=\frac {15a-1}{13} \le 500 \implies a \le \frac {500\times 13+1}{15} = 433.4\]

C’est $a$ qui limite, car la condition ci-dessus n’impose pas la limite 500 pour $b$.

Le plus petit $a$ qui convienne est $a=7$. Donc $a=7+13k$.

$7+13k \le 433 \implies k=32 \implies a=423$

$a=423$ est la plus grande valeur possible pour a. Ceci implique de facto $b=\frac{15\times 423-1}{13}=488$.

Finalement: $a+b=423+488=911$

Vérification en Python:

print(max((a + b, a, b)
          for a in range(501) for b in range(501)
          if 15 * a - 13 * b == 1))

réponse: 911

Vendredi 15 Juillet

On doit avoir 3 × a = 𝑥8, donc a = 6. On vérifie aisément que 6 est la solution: 6 + 66 + 666 = 738.

réponse: 6

Lundi 18 Juillet

Les triangles sont isocèles et rectangles (pour que les triangles remplissent le coin du rectangle).

Leur diagonale vaut donc 2√2. Et l’aire du rectangle: 3×2√2 × 2×2√2 = 48

réponse: 48 cm²

Mardi 19 Juillet

Il y a 9 barres noires et 8 blanches. Donc 8-3=5 barres noires épaisses et par conséquent 4 barres blanches fines.

réponse: 4

Mercredi 20 Juillet

Le vol dure 11h. Le repas est donc servi à 19h30.

réponse: 19h30

Jeudi 21 Juillet

Sur chaque extrêmité il y a 4 cordes : il faut donc 4×10=40 extrêmités de corde en tout. Et une corde a deux extrémités.

réponse: 20

Vendredi 22 Juillet

Les multiples de 3 qui ont pour chiffre des unités 6 sont $6+30k$ et ceux par 7 $27+30k$.

Multiples qui se terminent par 6: \(1 \le 6+30k \le 1000 \\ 0 \le k \le \lfloor \frac{1000-6}{30} \rfloor= 33 \\ \implies 34 \text{ valeurs}\)

Multiples qui se terminent par 7: \(1 \le 27+30k \le 1000 \\ 0 \le k \le \lfloor \frac{1000-27}{30} \rfloor= 32 \\ \implies 33 \text{ valeurs}\)

réponse: multiples qui finissent par 6

Lundi 25 Juillet

Le critère de divisibilité par 4 est que les deux derniers chiffres forment un nombre dvisible par 4. Avec les chiffres donnés, on peut former:

• 24
• 32, 36
• 52, 56
• 64
• 72, 76

Soit 8 terminaisons possibles. Avec les quatre autres chiffres, on peut former 4!=24 nombres par terminaison.

D’où 8×24 = 192 nombres

réponse: 192

Mardi 26 Juillet

Conditions:

• Rouge ≥ 1, Bleu ≥ 1, Vert ≥ 1
• Rouge + Vert ≥ 10
• Vert + Bleu ≥ 20
• Bleu + Rouge ≥ 40

Il faut au moins 41 billes: 40 bleues et rouges et 1 verte.

Exemple:

• 20 billes rouges
• 20 billes bleues
• 1 bille verte

réponse: 41

Mercredi 27 Juillet

• Il y a 12 triangles de côté 1.
• Il y a 6 triangles de côté 2.
• Il y a 2 triangles de côté 3.

réponse: 20

Jeudi 28 Juillet

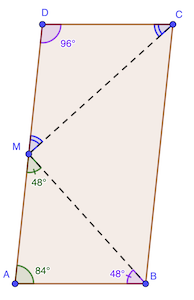
L’angle ∠ABM vaut 180 - 48 - 84 = 48°, donc le triangle ABM est isocèle en A.

AM = MD par définition et AB = DC parce que ABCD est un parallelogramme. Donc MDC est également isocèle en D.

L’angle ∠MDC vaut 180 - 84 = 96°, parce que ABCD est un parallélogramme. Et donc l’angle ∠DCM vaut (180 - 96) / 2 = 42°

réponse: 42°

Vendredi 29 Juillet

Posons: $X=x^{20}$ et $Y=y^{20}$

L’équation devient: $X^2-XY+Y^2=0$

$X=\frac 1 2 \left( Y \pm \sqrt {Y^2-4Y^2} \right)=\frac 1 2 Y \left( 1 \pm i \sqrt {3} \right)$

On voit que la seule solution réelle est Y=0 et X=0.

réponse: un couple: (0, 0)