Calendrier Mathématique Juin 2022
Mercredi 1 Juin
Soient $x,y$ tels que:
\[\frac 1 {x+1}+\frac 1 {y+1}=1\]Notons que $x \ne 0$ sinon il n’y a pas de solution.
\[y=\frac {1} {1-\frac 1 {x+1}}-1=\frac{x+1}{x+1-1}-1=\frac{1}{x}\]Remplaçons $x$ par $\frac 1 y$ dans l’équation:
\[\begin{aligned} \frac {1}{x-1}+\frac {1}{y-1}&= \frac {1}{ \frac 1 {y}-1}+\frac {1}{y-1} \\ &=\frac {y}{1-y}+\frac {1}{y-1} \\ &=\frac {1-y}{y-1} \\ &=-1 \end{aligned}\]réponse: -1
Jeudi 2 Juin
Il faut que le nombre soit divisible par 9 et par 2. Donc que la somme des chiffres soit multiple de 9 et le dernier chiffre pair.
∑ = 2+3+2+5+8+7+8 = 35
En enlèvent le premier 8 (et non le dernier!), on remplit les conditions.
réponse: 232578
Vendredi 3 Juin
L’angle en A du triangle rectangle est le complémentaire de 40°, soit 50°, parce que l’angle ∠CAB est droit.
Son autre angle non droit est à son tour le complémentaire de 50°, soit 40°.
réponse: x = 40°
Lundi 6 Juin
Si on prend comme premier chiffre 8, les autres s’imposent d’eux-mêmes: 876543210.
Si on prend comme premier chiffre 9, on doit enlever un des neuf autres chiffres. Soit neuf possibilités.
réponse: 10 possibilités
Mardi 7 Juin
E est le milieu de DC car la médiatrice de AB passe par E, coupe AB en son milieu de Thalès nous assure que E est bien dans la même proportion dans DC que le pied de la médiatrice dans AB.
Donc la hauteur du triangle AEB est (5+3)/2=4, sa base 7 et son aire 4×7/2=14 cm²
réponse: 14 cm²
Mercredi 8 Juin
réponse: 96 secondes, ou 1 min 36 secondes
Jeudi 9 Juin
En admettant qu’il n’y ait pas d’animal estropié, 14 ailes ⇒ 7 perroquets, 62 pattes ⇒ (62-2×7)/4=12 lapins, 24 têtes ⇒ (24-12-7)=5 serpents.
réponse: 5 serpents
Vendredi 10 Juin
Les carrés à un ou deux chiffres sont:
- 4: trop petit
- 9: 10 convient car 11 premier
- 16: 15 et 17 ne conviennent pas car 14 et 18 ne sont pas premiers, tous les carrés pairs ne peuvent donc convenir
- 25: 24 est ok (23 premier), mais pas 26 (27 non premier))
- 36: idem car pair
- 49: 48 est ok (47 premier), mais pas 50 (51 non premier)
- 64: idem car pair
- 81: 79 et 83 sont premiers
réponse: cinq nombres (10 24 48 80 82)
Lundi 13 Juin
La plus grande valeur pour ab est (-7)×(-5)=35 et pour c +6.
réponse: 41
Mardi 14 Juin
a7b + b8a + 9ac = 2022
- a + b + c = 2 ou 12 ou 22
- 7 + 8 + a + r₁ = 2 ou 12 ou 22
- a + b + 9 + r₂ = 20
De la deuxième équation, on voit qu’elle ne peut valoir que 22 (à cause du 15). Donc r₂ = 2, et a + b = 20 - 9 - 2 = 9.
La première équation devient 9 + c = 2 ou 12, donc c = 3, et r₁ = 1.
Par suite a = 6 et b = 3.
réponse: a=6 b=3 c=3
Mercredi 15 Juin
réponse: 1/5
Jeudi 16 Juin
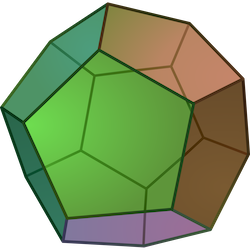
En coloriant les sommets de deux faces opposées, seules ces deux faces auront au moins trois sommets rouges, les autres n’en aurant que deux.
réponse: deux
Vendredi 17 Juin
\[a^3+2b^3-ba^2-2ab^2=0 \\ a^2(a-b) +a^2 b +2b^3-ba^2-2ab^2=0 \\ a^2(a-b)+ b^2( 2b-2a)=0 \\ (a-b)(a^2- 2b^2)=0\]Les solutions sont soit $a=b$ soit $a^2=2b^2$.
Seule $a=b$ donne des solutions entières.
réponse: 0
Lundi 20 Juin
Le petit côté des rectangles fait 1/√2 (puisque l’hypoténuse du triangle rectangle isocèlde fait 1).
Donc l’aire rouge: 1/√2 + 1 + 1/√2 = √2 + 1
Aire jaune: (1/√2)²/2 × 3 + 1/√2 × 2 = 3/4 + √2
réponse: 1/4 cm²
Mardi 21 Juin
réponse: 757252
Mercredi 22 Juin
On doit trouver a et b entiers tel que c soit entier: 2a+7b=5c
2a+7b = 2a+2b+5b
Il faut donc que 2(a+b) soit multiple de 5.
réponse: 5
Jeudi 23 Juin
réponse: 1 fille et 6 garçons, soit 7 élèves
Vendredi 24 Juin
Soit N le nombre de bananes très radioactives.
La probabilité de piocher dans une caisse avec ces bananes est 2/5. La proba d’avoir une banane radioactive est N/72 × 2/5.
N/72 × 2/5 = 0.05 ⇒ N = 72 × 0.05 × 5/2 = 9
réponse: 9 bananes
Lundi 27 Juin
\[\frac {x^3+y^3}{x+y}=x^2-xy+y^2=(x+y)^2-3xy\]En remplaçant par les valeurs de l’énoncé:
\[\frac {133}{7} = 7^2-3xy\] \[xy=\frac {7^3-133}{3\times 7}=\frac {210}{21}=10\]réponse: 10
Mardi 28 Juin
réponse: 41 × 32 = 1312
Mercredi 29 Juin
5 car tous les nombres à deux chiffres ou plus qui se terminent par 5 sont multiples de 5.
réponse: 5
Jeudi 30 Juin
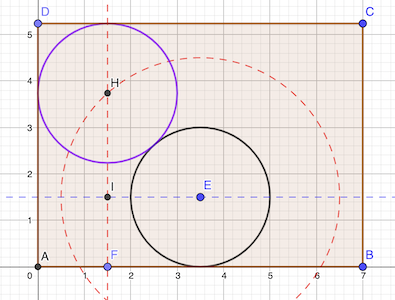
Pour être tangent au côté du rectangle et au cercle central C (noir), le centre H du cercle C1 (violet) doit être à l’intersection de la droite y=15 et du cercle de centre E et de rayon 30.
Le triangle EIH est rectangle en I, son hypoténuse est 30 et un de ses côtés 35 - 15 = 20. D’où IH = √(30² - 20²) = √500 = 10√5.
La longueur l = AD est donc 15 + 10√5 + 15 = 30 + 10√5 ≈ 52.4
réponse: 30+10√5 cm